Giải mục 2 trang 14, 15, 16 Chuyên đề học tập Toán 12 - Cánh diều

Hoạt động 2

Trả lời câu hỏi Hoạt động 2 trang 14 Chuyên đề học tập Toán 12 Cánh diều

a) Xét phép thử \(T\): “Tung một đồng xu cân đối và đồng chất một lần”. Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu. Viết không gian mẫu \(\Omega \) của phép thử \(T\).

b) Xét phép thử \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” (\({T_1}\) còn được gọi là phép thử lặp và việc tung một đồng xu hai lần liên tiếp một cách độc lập được hiểu là kết quả có thể xảy ra của lần thứ hai không phụ thuộc vào kết quả có thể xảy ra của tung lần thứ nhất).

Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu sau hai lần tung. Viết không gian mẫu \({\Omega _1}\) của phép thử \({T_1}\).

c) Trong phép thử lặp \({T_1}\) ta xét các biến cố:

\({A_0}\): “Mặt sấp không xuất hiện trong cả hai lần tung”;

\({A_1}\): “Mặt sấp xuất hiện một lần trong cả hai lần tung”;

\({A_2}\): “Mặt sấp xuất hiện hai lần trong cả hai lần tung”;

• Tính \(P({A_0})\); \(P({A_1})\); \(P({A_2})\)
• Với mỗi \(k = 0;1;2\) hãy so sánh: \(P({A_k})\) với \(C_2^k.{\left( {\frac{1}{2}} \right)^k}.{\left( {\frac{1}{2}} \right)^{2 - k}}\)

Phương pháp giải:

a,b: liệt kê các kết quả có thể xảy ra của phép thử.

c: Liệt kê các kết quả xảy ra của các biến cố \({A_0};{A_1};{A_2}\) từ đó tính xác suất xảy ra của các biến cố \({A_0};{A_1};{A_2}\).

Lời giải chi tiết:

a) Khi gieo đồng xu cân đối đồng chất thì sẽ có 2 trường hợp xảy ra là xuất hiện mặt sấp và xuất hiện mặt ngửa nên ta có không gian mẫu của phép thử \(T\)  là: \(\Omega  = \left\{ {S;\left. N \right\}} \right.\)

b) Khi gieo đồng xu 2 lần liên tiếp thì có thể xuất hiện 2 mặt sấp hoặc 2 mặt ngửa hoặc một mặt sấp một mặt ngửa nên ta có không gian mẫu của phép thử \({T_1}\) là: \({\Omega _1} = \{ SS;SN;NS;NN\} \)

c) Tính \(P({A_0})\); \(P({A_1})\); \(P({A_2})\)

Ta có biến cố \({A_0}\): “Mặt sấp không xuất hiện trong cả hai lần tung” nên ta có

\({A_0} = \{ NN\} \) \( \Rightarrow n({A_0}) = 1 \Rightarrow P({A_0}) = \frac{{n({A_0})}}{{n({\Omega _1})}} = \frac{1}{4}\)

Ta có biến cố \({A_1}\): “Mặt sấp xuất hiện một lần trong cả hai lần tung” nên ta có

\(\) \({A_1} = \{ SN;NS\} \) \( \Rightarrow n({A_1}) = 2 \Rightarrow P({A_1}) = \frac{{n({A_1})}}{{n({\Omega _1})}} = \frac{2}{4} = \frac{1}{2}\)

Ta có biến cố \({A_2}\): “Mặt sấp xuất hiện hai lần trong cả hai lần tung” nên ta có

\({A_2} = \{ SS\} \) \( \Rightarrow n({A_2}) = 1 \Rightarrow P({A_2}) = \frac{{n({A_2})}}{{n({\Omega _1})}} = \frac{1}{4}\)

• Với mỗi \(k = 0;1;2\) hãy so sánh: \(P({A_k})\) với \(C_2^k.{\left( {\frac{1}{2}} \right)^k}.{\left( {\frac{1}{2}} \right)^{2 - k}}\)

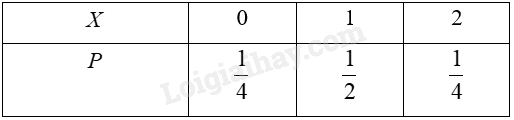
      +) Với \(k = 0\) ta có \(C_2^0.{\left( {\frac{1}{2}} \right)^0}.{\left( {\frac{1}{2}} \right)^{2 - 0}} = \frac{1}{4} = P({A_0})\)

      +) Với \(k = 1\) ta có \(C_2^1.{\left( {\frac{1}{2}} \right)^1}.{\left( {\frac{1}{2}} \right)^{2 - 1}} = \frac{1}{2} = P({A_1})\)

      +) Với \(k = 2\) ta có \(C_2^2.{\left( {\frac{1}{2}} \right)^2}.{\left( {\frac{1}{2}} \right)^{2 - 2}} = \frac{1}{4} = P({A_2})\)

      Vậy \(C_2^k.{\left( {\frac{1}{2}} \right)^k}.{\left( {\frac{1}{2}} \right)^{2 - k}} = P({A_k})\)

Hoạt động 3

Trả lời câu hỏi Hoạt động 3 trang 16 Chuyên đề học tập Toán 12 Cánh diều

Xét phép thử lặp \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập”. Gọi \(X\) là số lần mặt ngửa xuất hiện sau hai lần tung.

Lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\).

Phương pháp giải:

+)  \(X\) là số lần xuất hiện mặt ngửa của phép thử \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” nên \(X\) sẽ nhận các giá trị 0;1;2

+) Ta sẽ tính các xác suất: \(P(X = 0);P(X = 1);P(X = 2)\)

Lời giải chi tiết:

Gieo một đồng xu cân đối đồng chất hai lần liên tiếp thì có các khả năng sau xảy ra : \(SS;SN;NS;NN\)

Gọi \({A_k}\) là biến cố “Mặt ngửa xuất hiện đúng \(k\) lần”  \(k = 0;1;2\).

Vì xác suất xuất hiện mặt ngửa trong một lần tung là \(\frac{1}{2}\) nên ta áp dụng công thức Bernoulli với \(p = \frac{1}{2}\) và \(k = 0;1;2\) ta có:

\(P(X = 0) = P({A_0}) = C_2^0.{\left( {\frac{1}{2}} \right)^0}.{\left( {\frac{1}{2}} \right)^{2 - 0}} = \frac{1}{4}\);

\(P(X = 1) = P({A_1}) = C_2^1.{\left( {\frac{1}{2}} \right)^1}.{\left( {\frac{1}{2}} \right)^{2 - 1}} = \frac{1}{2}\)

\(P(X = 2) = P({A_2}) = C_2^2.{\left( {\frac{1}{2}} \right)^2}.{\left( {\frac{1}{2}} \right)^{2 - 2}} = \frac{1}{4}\)

Ta có bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\) như sau: