Giải mục 1 trang 34, 35, 36, 37, 38 Chuyên đề học tập Toán 12 - Kết nối tri thứcMột người đánh cá đang ở trên thuyền (vị trí A) cách bờ biển (điểm P) 2 km về phía đông trên đường bờ biển thẳng theo phương bắc nam. Nhà anh ấy nằm bên bờ biển, cách vị trí điểm P khoảng 6 km về phía bắc. Anh ấy có thể chèo thuyền với vận tốc 3 km/h và đi bộ với vận tốc 5 km/h (giả sử vận tốc của dòng nước là không đáng kể so với vận tốc mà người đánh cá chèo thuyền). Anh ấy dự kiến sẽ chèo thuyền thẳng đến một điểm Q đâu đó trên bờ biển về phía bắc điểm P, với 0 ≤ PQ ≤ 6 (km), rồi đi bộ quãng Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
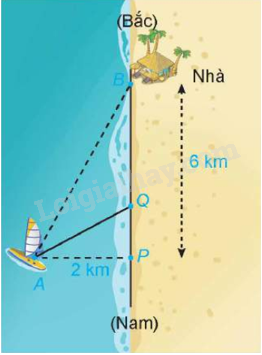
Hoạt động 1 Trả lời câu hỏi Hoạt động 1 trang 34 Chuyên đề học tập Toán 12 Kết nối tri thức Một người đánh cá đang ở trên thuyền (vị trí A) cách bờ biển (điểm P) 2 km về phía đông trên đường bờ biển thẳng theo phương bắc nam. Nhà anh ấy nằm bên bờ biển, cách vị trí điểm P khoảng 6 km về phía bắc. Anh ấy có thể chèo thuyền với vận tốc 3 km/h và đi bộ với vận tốc 5 km/h (giả sử vận tốc của dòng nước là không đáng kể so với vận tốc mà người đánh cá chèo thuyền). Anh ấy dự kiến sẽ chèo thuyền thẳng đến một điểm Q đâu đó trên bờ biển về phía bắc điểm P, với 0 ≤ PQ ≤ 6 (km), rồi đi bộ quãng đường còn lại để về nhà.
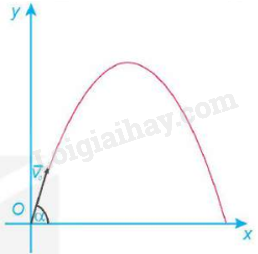
a) Hãy chọn các kí hiệu cho các đại lượng đã biết và đại lượng chưa biết trong bài toán trên. b) Tìm các mối quan hệ giữa các kí hiệu trong câu a). c) Nếu anh ấy chèo thuyền đến P rồi đi bộ về nhà thì hết bao nhiêu thời gian? d) Nếu anh ấy chèo thuyền đến điểm Q, rồi đi bộ về nhà thì hết bao nhiêu thời gian? Phương pháp giải: Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm. Lời giải chi tiết: a) Kí hiệu v1 là vận tốc chèo thuyền (v1 = 3 km/h) và v2 là vận tốc đi bộ (v2 = 5 km/h). Kí hiệu S1, v1 là quãng đường và vận tốc chèo thuyền của người đánh cá khi chèo thuyền. Kí hiệu S2, v2 là quãng đường và vận tốc của người đánh cá khi đi bộ dọc bờ biển. Ta có: v1 = 3 km/h, v2 = 5 km/h. Đặt \(PQ{\rm{ }} = {\rm{ }}x\) (km), \(x \in \left[ {0;6} \right]\). b) Ta có: \({S_2} = BQ = 6 - x{\rm{ }}(km)\) Vì tam giác APQ vuông tại P nên \({S_1} = AQ = \sqrt {A{P^2} + P{Q^2}} = \sqrt {4 + {x^2}} .\) c) Nếu anh ấy chèo thuyền đến P rồi đi bộ về nhà thì hết \(t = {t_{AP}} + {t_{PB}} = \frac{2}{3} + \frac{6}{5} = \frac{{28}}{{15}}\) (giờ) d) Nếu anh ấy chèo thuyền đến Q rồi đi bộ về nhà thì hết \(t = {t_{AQ}} + {t_{QB}} = \frac{{\sqrt {4 + {x^2}} }}{3} + \frac{{6 - x}}{5}\) (giờ) Luyện tập 1 Trả lời câu hỏi Luyện tập 1 trang 37 Chuyên đề học tập Toán 12 Kết nối tri thức Một vật được ném từ mặt đất lên trời xiên góc \(\alpha \) với phương nằm ngang với vận tốc ban đầu \({v_0}\; = 9{\rm{ }}m/s\)(Hình 2.10). Khi đó quỹ đạo chuyển động của vật tuân theo phương trình \(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) , ở đó x (mét) là khoảng cách vật bay được theo phương ngang từ điểm ném, y (mét) là độ cao so với mặt đất của vật trong quá trình bay, g là gia tốc trọng trường (theo Vật lí đại cương, Nhà xuất bản Giáo dục Việt Nam, 2016).
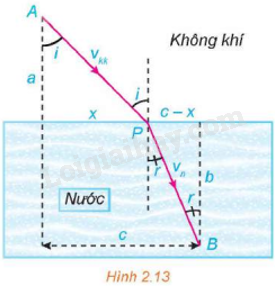
a) Tính độ cao nhất của vật trên quỹ đạo và xác định thời điểm mà vật đạt được độ cao đó (giả sử gia tốc trọng trường là g = 9,8 m/s2). b) Xác định góc ném α để tầm ném xa của vật đạt giá trị lớn nhất. Phương pháp giải: Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm. Lời giải chi tiết: a) Vì quỹ đạo chuyển động của vật có dạng hàm số bậc 2 đối với biến x có đồ thị là một parabol có bề lõi quay xuống dưới. Độ cao nhất của vật trên quỹ đạo ứng với tung độ đỉnh cao nhất của parabol Khi đó: \({x_p} = \frac{{ - \tan \alpha }}{{2.\frac{{ - g}}{{2.v_0^2{\rm{co}}{{\rm{s}}^2}\alpha }}}} = \sin \alpha .\cos \alpha .\frac{{v_0^2}}{g};{y_P} = {\sin ^2}\alpha .\frac{{v_0^2}}{{2g}}\) Tại \({v_0} = 9\)(m/s), ta có độ cao lớn nhất của vật là: \({y_P} = {\sin ^2}\alpha .\frac{{405}}{{98}}\) Thời điểm vật đạt được độ cao lớn nhất là: \(t = \frac{{{x_p}}}{{{v_0}.\cos \alpha }} = \frac{{{v_0}}}{g}\sin \alpha = \frac{{45}}{{49}}\sin \alpha \) b) Tầm ném xa trong chuyển động ném xiên là: \(L = 2{x_p} = \sin 2\alpha .\frac{{v_0^2}}{g} = \frac{{810}}{{98}}\sin 2\alpha \le \frac{{405}}{{49}}\). Tầm ném xa đạt giá trị lớn nhất bằng \(\frac{{405}}{{49}}\) khi \(\sin 2\alpha = 1\) hay \(\alpha = \frac{\pi }{4}\). Luyện tập 2 Trả lời câu hỏi Luyện tập 2 trang 38 Chuyên đề học tập Toán 12 Kết nối tri thức Gọi \({v_{kk}}\) là vận tốc ánh sáng trong không khí và \({v_n}\) là vận tốc ánh sáng trong nước. Theo nguyên lí Fermat, một tia sáng di chuyển từ một điểm A trong không khí đến một điểm B trong nước theo đường gấp khúc APB sao cho tổng thời gian di chuyển là nhỏ nhất (Hình 2.13). Vận dụng đạo hàm tìm vị trí cực trị của hàm số T(x) (tổng thời gian tia sáng đi từ A đến B theo đường gấp khúc APB) để chứng tỏ rằng khi T(x) nhỏ nhất thì góc tới i và góc khúc xạ r thỏa mãn phương trình \(\frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}\). Phương trình này được gọi là Định luật Snell.
Phương pháp giải: Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm. Lời giải chi tiết: Từ hình vẽ, với 0 ≤ x ≤ c ta có: \(AP = \sqrt {{a^2} + {x^2}} \) và \(PB = \sqrt {{b^2} + {{(c - x)}^2}} .\) Thời gian ánh sáng di chuyển từ A đến P là: \({t_1} = \frac{{AP}}{{{v_{kk}}}} = \frac{{\sqrt {{a^2} + {x^2}} }}{{{v_{kk}}}}.\) . Thời gian ánh sáng di chuyển từ P đến B là: \({t_2} = \frac{{PB}}{{{v_n}}} = \frac{{\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}{{{v_n}}}.\) Khi đó, tổng thời gian tia sáng đi từ A đến B theo đường gấp khúc APB là: \(T\left( x \right) = {t_1} + {t_2} = \frac{{\sqrt {{a^2} + {x^2}} }}{{{v_{kk}}}} + \frac{{\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}{{{v_n}}},0 \le x \le c.\) Đạo hàm của hàm T(x) là: \(T'\left( x \right) = \frac{x}{{{v_{kk}}\sqrt {{a^2} + {x^2}} }} - \frac{{c - x}}{{{v_n}\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}.\) Ta có \(\begin{array}{l}T'\left( x \right) = 0 \Leftrightarrow \frac{x}{{{v_{kk}}\sqrt {{a^2} + {x^2}} }} = \frac{{c - x}}{{{v_n}\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}.\\ \Leftrightarrow \frac{1}{{{v_{kk}}}} \cdot \frac{x}{{\sqrt {{a^2} + {x^2}} }} = \frac{1}{{{v_n}}} \cdot \frac{{c - x}}{{\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}\\ \Leftrightarrow \frac{1}{{{v_{kk}}}}\sin i = \frac{1}{{{v_n}}}\sin r \Leftrightarrow \frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}.\end{array}\) Giả sử x = x0 thỏa mãn \(\frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}\) Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có: \(T\left( 0 \right) = \frac{a}{{{v_{kk}}}} + \frac{{\sqrt {{b^2} + {c^2}} }}{{{v_n}}};\,\,T\left( {{x_0}} \right) = \frac{{\sqrt {{a^2} + x_0^2} }}{{{v_{kk}}}} + \frac{{\sqrt {{b^2} + {{\left( {c - {x_0}} \right)}^2}} }}{{{v_n}}};\,\,T\left( c \right) = \frac{{\sqrt {{a^2} + {c^2}} }}{{{v_{kk}}}} + \frac{b}{{{v_n}}}.\) Ta có T(x0) là giá trị nhỏ nhất trong các giá trị T(0), T(x0), T(c). Vậy T(x) nhỏ nhất khi góc tới i và góc khúc xạ r thỏa mãn phương trình \(\frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}\).
|




















Danh sách bình luận