Giải bài 2.7 trang 42 Chuyên đề học tập Toán 12 - Kết nối tri thứcNgười ta muốn kéo một đường dây điện tử nhà máy điện đặt tại điểm A đến một hòn đảo nhỏ C. Biết rằng nhà máy điện nằm sát bờ biển, bờ biển được coi là thẳng, khoảng cách CB từ hòn đảo C đến bờ biển là 1 km, khoảng cách giữa hai điểm A và B là 4 km. Mỗi kilômét dây nếu đặt ngầm dưới nước sẽ mất 5 000 USD, còn nếu đặt ngầm dưới đất sẽ mất 3 000 USD. Người ta dự định kéo dây điện ngầm dưới đất từ điểm A đến một điểm S trên bờ biển, nằm giữa A và B, sau đó chạy ngầm dưới nước từ điểm S đến hòn đảo C Quảng cáo
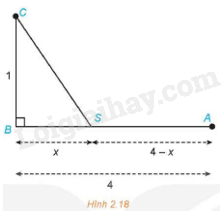
Đề bài Người ta muốn kéo một đường dây điện tử nhà máy điện đặt tại điểm A đến một hòn đảo nhỏ C. Biết rằng nhà máy điện nằm sát bờ biển, bờ biển được coi là thẳng, khoảng cách CB từ hòn đảo C đến bờ biển là 1 km, khoảng cách giữa hai điểm A và B là 4 km. Mỗi kilômét dây nếu đặt ngầm dưới nước sẽ mất 5 000 USD, còn nếu đặt ngầm dưới đất sẽ mất 3 000 USD. Người ta dự định kéo dây điện ngầm dưới đất từ điểm A đến một điểm S trên bờ biển, nằm giữa A và B, sau đó chạy ngầm dưới nước từ điểm S đến hòn đảo C (Hình 2.18). Tìm vị trí điểm S sao cho chi phí kéo đường dây là nhỏ nhất.
Phương pháp giải - Xem chi tiết Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm. Lời giải chi tiết Đặt \(BS = x{\rm{ }}(m)\)\((0 \le x \le 4)\). Khi đó, \(SA = 4 - x;CS = \sqrt {1 + {x^2}} \) Khi đó, chi phí cần bỏ ra là: \(f(x) = 5{\rm{ }}000\sqrt {1 + {x^2}} + 3{\rm{ }}000(4 - x)\), \(x \in \left[ {0;4} \right]\) \(f'(x) = \frac{{5{\rm{ }}000x}}{{\sqrt {1 + {x^2}} }} - 3{\rm{ }}000\) \(f'(x) = 0 \Leftrightarrow 3\sqrt {1 + {x^2}} = 5x \Leftrightarrow x = \frac{3}{4}\) Ta có \(f(0) = 17{\rm{ }}000;f\left( {\frac{3}{4}} \right) = 16{\rm{ }}000;f(4) \approx 20{\rm{ }}616\). Ta thấy GTNN ứng với \(x = \frac{3}{4}\). Vậy điểm S trên bờ biển cần tìm cách A một khoảng \(4 - \frac{3}{4} = \frac{{13}}{4}(km)\).  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
