Giải mục 1 trang 11 Chuyên đề học tập Toán 11 - Chân trời sáng tạoQuan sát các điểm được vẽ trên mặt phẳng tọa độ (Hình 1). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
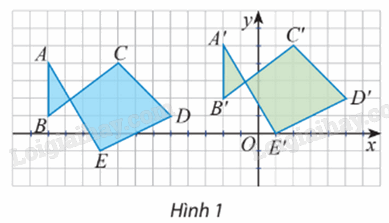
Khám phá 1 Quan sát các điểm được vẽ trên mặt phẳng tọa độ (Hình 1). a) Có nhận xét gì về các vectơ \(\overrightarrow {AA'} ,\,\overrightarrow {BB'} ,\,...,\,\overrightarrow {EE'} \) b) Có hay không phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’?
Phương pháp giải: Quan sát hình 1, nhận xét về hướng, độ dài của các vectơ Lời giải chi tiết:
a) Quan sát Hình 1, ta thấy các vectơ \(\overrightarrow {AA'} ,\,\overrightarrow {BB'} ,\,...,\,\overrightarrow {EE'} \) cùng hướng và có độ dài bằng nhau. Vậy \(\overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \) b) Ta đặt \({\rm{\vec u}} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \) Khi đó tồn tại phép biến hình biến điểm A thành điểm A’ sao cho \(\overrightarrow {AA'} = {\rm{\vec u}}\) Tương tự như vậy, ta thấy phép biến hình đó cũng biến các điểm B, C, D, E thành các điểm B’, C’, D’, E’ sao cho \(\overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} = {\rm{\vec u}}\) Vậy có phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’ Thực hành 1 Chứng minh phép đồng nhất là một phép tịnh tiến. Phương pháp giải: Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \). Lời giải chi tiết: Giả sử A’ là ảnh của A qua phép đồng nhất f. Tức là, A’ = f(A). Suy ra \(A'{\rm{ }} \equiv {\rm{ }}A\) hay \(AA'{\rm{ }} = {\rm{ }}0.\) Khi đó \(\overrightarrow {AA'} = \vec 0\). Tương tự như vậy, với mỗi điểm M bất kì, ta lấy điểm M’ là ảnh của điểm M qua phép đồng nhất f. Khi đó ta cũng có \(\overrightarrow {MM'} = \vec 0\). Vậy phép đồng nhất là một phép tịnh tiến theo \(\vec 0\) Vận dụng 1 Tìm độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) biến các điểm A, B, C, D, E thành A’, B’, C’, D’, E’ trong Hoạt động khám phá 1 (biết cạnh mỗi ô vuông là 1 đơn vị). Phương pháp giải: Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \). Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\) Lời giải chi tiết: Từ Hoạt động khám phá 1, ta có \({\rm{\vec u}} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \). Ta đặt \({\rm{\vec v}} = {\rm{\vec u}}\) Khi đó phép tịnh tiến theo \({\rm{\vec v}} = {\rm{\vec u}}\) biến các điểm A, B, C, D, E thành điểm A’, B’, C’, D’, E’. Dựng \(\Delta AA'M\) vuông tại M (như hình vẽ).
Ta có \(AM{\rm{ }} = {\rm{ }}1\) (đơn vị), \(A'M{\rm{ }} = {\rm{ }}10\) (đơn vị) (do cạnh mỗi ô vuông là 1 đơn vị). Suy ra \(AA' = \sqrt {A{M^2} + {\rm{A'}}{{\rm{M}}^2}} = \sqrt {{1^2} + {{10}^2}} = \sqrt {101} \). Khi đó \(\left| {{\rm{\vec v}}} \right| = \left| {\overrightarrow {AA'} } \right| = AA' = \sqrt {101} \) Vậy độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) là \(\sqrt {101} \).
|






















Danh sách bình luận