Giải bài 2 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạoCho đường tròn (O) và hai điểm A, B. Khi điểm M thay đổi trên đường tròn (O) thì điểm M’ thay đổi trên đường nào để \(\overrightarrow {MM'} + \overrightarrow {MA} = \overrightarrow {MB} \)? Quảng cáo
Đề bài Cho đường tròn (O) và hai điểm A, B. Khi điểm M thay đổi trên đường tròn (O) thì điểm M’ thay đổi trên đường nào để \(\overrightarrow {MM'} + \overrightarrow {MA} = \overrightarrow {MB} \)? Phương pháp giải - Xem chi tiết Vẽ hình và sử dụng quy tắc hình bình hành để làm Lời giải chi tiết
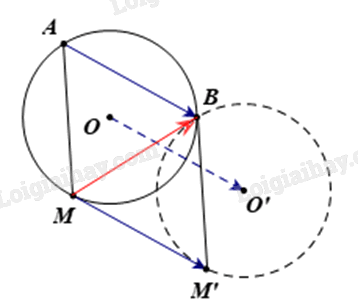
Do A, B cố định nên \(\overrightarrow {AB} \) là vectơ không đổi. Từ dữ kiện \(\overrightarrow {MM'} + \overrightarrow {MA} = \overrightarrow {MB} \), áp dụng quy tắc hình bình hành, ta có tứ giác ABM’M là hình bình hành. Do đó \(\overrightarrow {MM'} = \overrightarrow {AB} \) Vì vậy M’ là ảnh của M qua phép tịnh tiến \({T_{\overrightarrow {AB} }}\). Vậy khi M thay đổi trên đường tròn (O) thì M’ nằm trên ảnh của đường tròn (O) là đường tròn (O’) qua phép tịnh tiến \({T_{\overrightarrow {AB} }}\).
|