Giải đề thi học kì 2 toán lớp 11 năm 2019 - 2020 trường THPT Kim Liên - Hà Nội

PHẦN I: TRẮC NGHIỆM (5 điểm)

Câu 1. Cho tứ diện ABCD với M là trung điểm cạnh BC. Mệnh đề nào sau đây sai?

A. \(\overrightarrow {AB}  + \overrightarrow {AC}  = 2\overrightarrow {AM} \)

B. \(\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD}  = \overrightarrow 0 \)

C. \(\overrightarrow {MD}  =  - \frac{1}{2}\left( {\overrightarrow {DB}  + \overrightarrow {DC} } \right)\)

D. \(\overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \)

Câu 2. Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\), đáy \(ABC\) là tam giác vuông tại đỉnh C. Gọi AH, AK lần lượt là đường cao các tam giác SAB, SAC. Khẳng định nào dưới đây đúng?

A. K là hình chiếu vuông góc của A trên mặt phẳng (SBC)

B. H là hình chiếu vuông góc của A trên mặt phẳng (SBC)

C. B là hình chiếu vuông góc của C trên mặt phẳng (SAB)

D. A là hình chiếu vuông góc của S trên mặt phẳng (AHK)

Câu 3.  Trong các giới hạn sau đây, giới hạn nào bằng 2?

A. \(\lim \left( {2{n^2} + n + 3} \right)\)

B. \(\lim \frac{{2{n^5} - {n^4}}}{{ - 3{n^3} + {n^5}}}\)

C. \(\lim \frac{{2{n^2} + 1}}{{{n^4} + 3}}\)

D. \(\lim \frac{{{n^3} - 1}}{{ - 2{n^2} + 4{n^3}}}\)

Câu 4.  Bảo tàng Hà Nội được xây dựng gồm hai tầng hầm và bốn tầng nổi. Bốn tầng nổi được dùng để trưng bày rất nhiều những hiện vật có giá trị. Diện tích sàn tầng nổi thứ nhất xấp xỉ \(12\,000\,{m^2}\). Biết rằng mỗi tầng nổi tiếp theo có diện tích bằng \(\frac{4}{3}\) diện tích nổi ngay dưới nó. Tính tổng diện tích mặt sàn của bốn tầng nổi dùng để trưng bày hiện vật của bảo tàng (làm tròn đến hàng đơn vị).

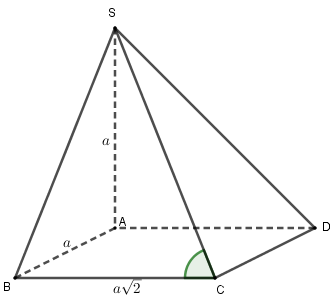
A. \(37\,926\,{m^2}\)

B. \(77\,778\,{m^2}\)

C. \(77\,777\,{m^2}\)

D. \(48\,008\,{m^2}\)

Câu 5.  Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng 2a. Tính cosin của góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {ABCD} \right)\).

A. \(\frac{{\sqrt {210} }}{{15}}\)

B. \(\frac{1}{3}\)

C. \(\frac{{\sqrt {15} }}{{15}}\)

D. \(\frac{1}{4}\)

Câu 6.  Tìm tham số a để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{x^2} + 5}  - 3}}{{x + 2}}\,\,\,khi\,\,\,x \ne  - 2\\ax + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,x =  - 2\end{array} \right.\) liên tục tại \({x_0} =  - 2\)

A. \(a = \frac{{10}}{3}\)

B. \(a = \frac{2}{3}\)

C. \(a =  - \frac{5}{6}\)

D. \(a = \frac{5}{6}\)

Câu 7.  Cho cấp số cộng \(\left( {{u_n}} \right)\) biết \({u_1} =  - 7,{S_{20}} = 620\). Tìm công sai \(d\)?

A. \(4\)

B. \(\frac{{45}}{{19}}\)

C. \(\frac{{19}}{5}\)

D. \(\frac{{69}}{{19}}\)

Câu 8.  \(\lim \frac{{2n + 1}}{{n - 3}}\) bằng

A. \( - \frac{1}{3}\)

B. \( + \infty \)

C. \(\frac{1}{2}\)

D. \(2\)

Câu 9.  Một điểm chuyển động thẳng, quãng đường đi được xác định bởi phương trình \(s\left( t \right) = {t^3} + 5{t^2} - 6t + 3\) (t tính bằng giây, s tính bằng mét). Tính vận tốc của chất điểm tại thời điểm \(t = 3\).

A. \(57\,m/s\)

B. \(51\,m/s\)

C. \(42\,m/s\)

D. \(39\,m/s\)

Câu 10.  Trong các dãy số \(\left( {{u_n}} \right)\) sau đây, dãy số giảm là

A. \({u_n} = \sin n\)

B. \({u_n} = \sqrt n  - \sqrt {n - 1} \)

C. \({u_n} = {\left( { - 1} \right)^n}\left( {{2^n} + 1} \right)\)

D. \({u_n} = \frac{{{n^2} + 1}}{n}\)

Câu 11.  Cho hàm số \(f\left( x \right) = {x^3} - 3{x^2} + 2020\). Tìm tập nghiệm \(S\) của bất phương trình \(f'\left( x \right) \le 0\).

A. \(S = \left( { - \infty ;0} \right] \cup \left[ {2; + \infty } \right)\)

B. \(S = \left[ {2; + \infty } \right)\)

C. \(S = \left( {0;2} \right)\)

D. \(S = \left[ {0;2} \right]\)

Câu 12.  Biết \(\mathop {\lim }\limits_{x \to  - \infty } \left( {ax + \sqrt {{x^2} + bx + 1} } \right) = \frac{1}{2}\). Tính \(A = 2a + b\)

A. \( - 1\)

B. \(2\)

C. \(0\)

D. \(1\)

Câu 13.  Cho cấp số nhân \(\left( {{u_n}} \right)\) biết \({u_1} =  - 3,{u_2} = 6\). Tìm \({u_5}\).

A. \({u_5} =  - 24\)

B. \({u_5} = 48\)

C. \({u_5} =  - 48\)

D. \({u_5} = 24\)

Câu 14.  Trong bốn giới hạn sau đây, giới hạn nào là \( - \infty \)?

A. \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{ - x + 4}}{{x - 1}}\)

B. \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{ - x + 4}}{{x - 1}}\)

C. \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{ - x + 4}}{{x - 1}}\)

D. \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{ - x + 4}}{{x - 1}}\)

Câu 15.  Cho hình chóp tứ giác \(S.ABCD\) có SA vuông góc với mặt phẳng (ABCD). Đáy \(ABCD\) là hình chữ nhật, \(SA = AB = a,BC = a\sqrt 2 \). Gọi \(\alpha \) là góc giữa hai đường thẳng \(AD\) và \(SC\). Tính số đo góc \(\alpha \).

A. \(\alpha  = {135^0}\)

B. \(\alpha  = {45^0}\)

C. \(\alpha  = {90^0}\)

D. \(\alpha  = {60^0}\)

Câu 16.  Đạo hàm của hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) là

A. \(y' = \frac{{2x + 2}}{{{{\left( {x + 1} \right)}^2}}}\)

B. \(y' = 2x + 2\)

C. \(y' = \frac{{{x^2} + 2x}}{{x + 1}}\)

D. \(y' = \frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}}\)

Câu 17.  Cho hình lập phương \(ABCD.A'B'C'D'\). Mệnh đề nào sau đây sai?

A. \(B'D \bot AA'\)

B. \(B'D \bot AD'\)

C. \(B'D \bot \left( {ACD'} \right)\)

D. \(AB \bot B'C'\)

Câu 18.  Cho hàm số \(y = {x^3} + 3{x^2} - 1\) có đồ thị \(\left( C \right)\). Viết phương trình tiếp tuyến của \(\left( C \right)\) tại điểm M có hoành độ bằng \( - 1\)

A. \(y = 3x - 2\)

B. \(y =  - 3x - 2\)

C. \(y = 3x + 2\)

D. \(y =  - 3x + 2\)

Câu 19.  Trong các dãy số sau đây, dãy số nào là cấp số cộng?

A. \(\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = 2{u_n}\end{array} \right.\)

B. \(\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = {u_n} + n\end{array} \right.\)

C. \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = u_n^3 - 2\end{array} \right.\)

D. \(\left\{ \begin{array}{l}{u_1} =  - 1\\{u_{n + 1}} - {u_n} = 2\end{array} \right.\)

Câu 20.  Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a\), cạnh bên \(AA' = \frac{{3a}}{2}\) (tham khảo hình vẽ bên). Tính khoảng cách từ điểm \(C'\) đến mặt phẳng \(\left( {CA'B'} \right)\).

A. \(\frac{{2a}}{{\sqrt 3 }}\)

B. \(\frac{{3a}}{2}\)

C. \(\frac{{a\sqrt 3 }}{4}\)

D. \(\frac{{3a}}{4}\)

PHẦN II: TỰ LUẬN (5 điểm)

Câu 1 (1,0 điểm). Tổng ba số hạng liên tiếp của một cấp số cộng bằng \(45\). Nếu bớt 6 đơn vị ở số hạng thứ hai và giữ nguyên các số còn lại thì được một cấp số nhân. Tìm ba số đó.

Câu 2 (2,0 điểm). Cho hàm số \(y = f\left( x \right)\) \( = 2{x^3} - 3{x^2} + 7x - 15\).

a) Giải bất phương trình \(f'\left( x \right) > 0\).

b) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến đó song song với đường thẳng \(y = 7x - 15\)

Câu 3 (2,0 điểm). Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh \(a\). Hai mặt phẳng \(\left( {SAB} \right),\left( {SAD} \right)\) cùng vuông góc với mặt phẳng đáy, \(SA = 2a\).

a) Chứng minh rằng \(\left( {SAC} \right) \bot \left( {SBD} \right)\)

b) Xác định và tính tang của góc giữa đường thẳng \(SC\) và \(\left( {ABCD} \right)\).

c) Gọi \(M\) là trung điểm của \(AD\). Tính khoảng cách từ điểm \(O\) đến mặt phẳng \(\left( {SMC} \right)\).

------- HẾT -------

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

PHẦN I: TRẮC NGHIỆM (5 điểm)

Câu 1 (TH):

Phương pháp:

Gọi N là trung điểm của AD, kiểm tra tính đúng sai của từng đáp án.

Cách giải:

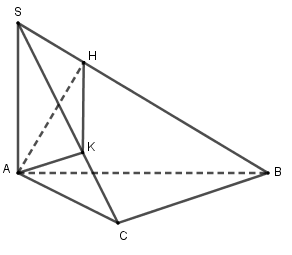
Đáp án A: \(\overrightarrow {AB}  + \overrightarrow {AC}  = 2\overrightarrow {AM} \) đúng.

Đáp án B:

\(\begin{array}{l}\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD} \\ = \left( {\overrightarrow {MA}  + \overrightarrow {MD} } \right) + \left( {\overrightarrow {MB}  + \overrightarrow {MC} } \right)\\ = 2\overrightarrow {MN}  + \overrightarrow 0 \\ = 2\overrightarrow {MN}  \ne \overrightarrow 0 \end{array}\)

Nên B sai.

Đáp án C: \(\overrightarrow {DB}  + \overrightarrow {DC}  = 2\overrightarrow {DM} \)\( \Rightarrow \overrightarrow {DM}  = \frac{1}{2}\left( {\overrightarrow {DB}  + \overrightarrow {DC} } \right)\)  \( \Rightarrow \overrightarrow {MD}  =  - \frac{1}{2}\left( {\overrightarrow {DB}  + \overrightarrow {DC} } \right)\) nên C đúng.

Đáp án D: \(\overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \) đúng.

Chọn B.

Câu 2 (TH):

Phương pháp:

Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau cùng thuộc mặt phẳng.

Cách giải:

Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)

Mà \(BC \bot AC\) (do \(\Delta ABC\) vuông tại \(C\))

\( \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot AK\)

Lại có \(AK \bot SC\left( {gt} \right)\) nên \(AK \bot \left( {SBC} \right)\).

Vậy K là hình chiếu của A lên \(\left( {SBC} \right)\).

Chọn A

Câu 3 (TH):

Phương pháp:

Tính từng giới hạn và nhận xét.

Cách giải:

Đáp án A: \(\lim \left( {2{n^2} + n + 3} \right) =  + \infty \) nên loại.

Đáp án B:

\(\begin{array}{l}\lim \frac{{2{n^5} - {n^4}}}{{ - 3{n^3} + {n^5}}}\\ = \lim \frac{{{n^5}\left( {2 - \frac{1}{n}} \right)}}{{{n^5}\left( { - \frac{3}{{{n^2}}} + 1} \right)}}\\ = \lim \frac{{\left( {2 - \frac{1}{n}} \right)}}{{\left( { - \frac{3}{{{n^2}}} + 1} \right)}} = \frac{{2 - 0}}{{0 + 1}} = 2\end{array}\)

Chọn B

Câu 4 (TH):

Phương pháp:

Sử dụng công thức tính tổng cấp số nhân \({S_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\)

Cách giải:

Diện tích 4 tầng nổi tạo thành một CSN có công bội \(q = \frac{4}{3}\) và \({u_1} = 12\,\,000\).

Tổng diện tích 4 tầng nổi là:

\(\begin{array}{l}{S_4} = \frac{{{u_1}\left( {1 - {q^4}} \right)}}{{1 - q}}\\ = \frac{{12\,\,000\left( {1 - {{\left( {\frac{4}{3}} \right)}^4}} \right)}}{{1 - \frac{4}{3}}}\\ \approx 77\,\,778\left( {{m^2}} \right)\end{array}\)

Chọn B

Câu 5 (TH):

Phương pháp:

Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến.

Cách giải:

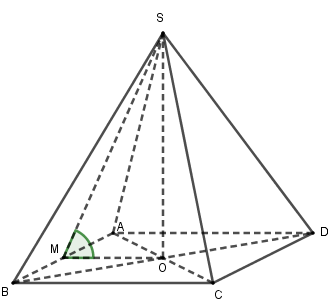
Gọi M là trung điểm của AB ta có:

\(\left\{ \begin{array}{l}\left( {SAB} \right) \supset SM \bot AB\\\left( {ABCD} \right) \supset OM \bot AB\end{array} \right.\) \( \Rightarrow \) góc giữa \(\left( {SAB} \right)\) và \(\left( {ABCD} \right)\) bằng góc giữa \(SM\) và \(OM\).

Ta có:

\(\begin{array}{l}OM = \frac{1}{2}BC = \frac{a}{2}\\SM = \sqrt {S{A^2} - A{M^2}} \\ = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {\frac{a}{2}} \right)}^2}}  = \frac{{a\sqrt {15} }}{2}\\ \Rightarrow \cos \widehat {SMO} = \frac{{OM}}{{AM}} = \frac{{\frac{a}{2}}}{{\frac{{a\sqrt {15} }}{2}}} = \frac{{\sqrt {15} }}{{15}}\end{array}\)

Chọn C

Câu 6 (VD):

Phương pháp:

Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0}\) \( \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Cách giải:

Ta có:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to  - 2} f\left( x \right) = \mathop {\lim }\limits_{x \to  - 2} \frac{{\sqrt {{x^2} + 5}  - 3}}{{x + 2}}\\ = \mathop {\lim }\limits_{x \to  - 2} \frac{{{x^2} + 5 - 9}}{{\left( {x + 2} \right)\left( {\sqrt {{x^2} + 5}  + 3} \right)}}\\ = \mathop {\lim }\limits_{x \to  - 2} \frac{{{x^2} - 4}}{{\left( {x + 2} \right)\left( {\sqrt {{x^2} + 5}  + 3} \right)}}\\ = \mathop {\lim }\limits_{x \to  - 2} \frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {x + 2} \right)\left( {\sqrt {{x^2} + 5}  + 3} \right)}}\\ = \mathop {\lim }\limits_{x \to  - 2} \frac{{x - 2}}{{\sqrt {{x^2} + 5}  + 3}}\\ = \frac{{ - 2 - 2}}{{\sqrt {{{\left( { - 2} \right)}^2} + 5}  + 3}}\\ =  - \frac{2}{3}\\f\left( { - 2} \right) =  - 2a + 1\end{array}\)

Hàm số liên tục tại \(x =  - 2\)

\(\begin{array}{l} \Leftrightarrow \mathop {\lim }\limits_{x \to  - 2} f\left( x \right) = f\left( { - 2} \right)\\ \Leftrightarrow  - \frac{2}{3} =  - 2a + 1\\ \Leftrightarrow  - 2a =  - \frac{5}{3}\\ \Leftrightarrow a = \frac{5}{6}\end{array}\)

Chọn D

Câu 7 (TH):

Phương pháp:

Sử dụng công thức tổng n số hạng đầu của CSC: \({S_n} = \frac{{n\left( {2{u_1} + \left( {n - 1} \right)d} \right)}}{2}\)

Cách giải:

Ta có:

\(\begin{array}{l}{S_{20}} = \frac{{20\left( {2{u_1} + 19d} \right)}}{2}\\ \Leftrightarrow 620 = \frac{{20\left[ {2.\left( { - 7} \right) + 19d} \right]}}{2}\\ \Leftrightarrow 20\left( { - 14 + 19d} \right) = 1240\\ \Leftrightarrow  - 14 + 19d = 62\\ \Leftrightarrow 19d = 76\\ \Leftrightarrow d = 4\end{array}\)

Chọn A

Câu 8 (TH):

Phương pháp:

Chia cả tử và mẫu cho \(n\).

Cách giải:

Ta có: \(\lim \frac{{2n + 1}}{{n - 3}} = \lim \frac{{2 + \frac{1}{n}}}{{1 - \frac{3}{n}}} = 2\)

Chọn D

Câu 9 (TH):

Phương pháp:

Sử dụng công thức \(v\left( t \right) = s'\left( t \right)\).

Cách giải:

Ta có:

\(\begin{array}{l}v\left( t \right) = s'\left( t \right)\\ = \left( {{t^3} + 5{t^2} - 6t + 3} \right)'\\ = 3{t^2} + 5.2t - 6.1\\ = 3{t^2} + 10t - 6\end{array}\)

Với \(t = 3\) thì \(v\left( 3 \right) = {3.3^2} + 10.3 - 6 = 51\) (m/s)

Chọn B

Câu 10 (VD):

Phương pháp:

Nhận xét từng đáp án, có thể lấy phản ví dụ cho các đáp án sai.

Dãy số \(\left( {{u_n}} \right)\) là dãy số giảm nếu \({u_{n + 1}} < {u_n}\) với mọi \(n \in {\mathbb{N}^*}\).

Cách giải:

Đáp án A: sai vì \({u_1} = \sin 1 < \sin 2 = {u_2}\) nên dãy này không giảm.

Đáp án B:

\(\begin{array}{l}{u_n} = \sqrt n  - \sqrt {n - 1} \\ = \frac{{n - \left( {n - 1} \right)}}{{\sqrt n  + \sqrt {n - 1} }}\\ = \frac{1}{{\sqrt n  + \sqrt {n - 1} }}\\{u_{n + 1}} - {u_n}\\ = \frac{1}{{\sqrt {n + 1}  + \sqrt n }} - \frac{1}{{\sqrt n  + \sqrt {n - 1} }}\end{array}\)

Vì \(\sqrt {n + 1}  > \sqrt {n - 1} \) nên

\(\begin{array}{l}\sqrt {n + 1}  + \sqrt n  > \sqrt n  + \sqrt {n - 1} \\ \Rightarrow \frac{1}{{\sqrt {n + 1}  + \sqrt n }} < \frac{1}{{\sqrt n  + \sqrt {n - 1} }}\\ \Rightarrow \frac{1}{{\sqrt {n + 1}  + \sqrt n }} - \frac{1}{{\sqrt n  + \sqrt {n - 1} }} < 0\\ \Rightarrow {u_{n + 1}} < {u_n}\end{array}\)

Do đó dãy số giảm.

Đáp án C: sai vì đây là dãy đan dấu nên không giảm cũng không tăng.

Cụ thể: \({u_{2k}} = {2^{2k}} + 1 > 0,\) \({u_{2k + 1}} =  - \left( {{2^{2k + 1}} + 1} \right) < 0\).

Đáp án D: sai vì \({u_1} = 2;{u_2} = \frac{5}{2} \Rightarrow {u_1} < {u_2}\).

Chọn B

Câu 11 (TH):

Phương pháp:

Tính \(f'\left( x \right)\) và giải bất phương trình \(f'\left( x \right) \le 0\).

Cách giải:

Ta có: \(f'\left( x \right) = 3{x^2} - 6x\)

\(\begin{array}{l}f'\left( x \right) \le 0 \Leftrightarrow 3{x^2} - 6x \le 0\\ \Leftrightarrow 0 \le x \le 2\end{array}\)

Vậy \(S = \left[ {0;2} \right]\)

Chọn D

Câu 12 (VDC):

Phương pháp:

Biện luận giới hạn vế trái theo \(a\).

Cách giải:

Dễ thấy nếu \(a \le 0\) thì \(\mathop {\lim }\limits_{x \to  - \infty } \left( {ax + \sqrt {{x^2} + bx + 1} } \right) =  + \infty \) nên không thỏa mãn.

Ta xét \(a > 0\).

Đặt

\(\begin{array}{l}L = \mathop {\lim }\limits_{x \to  - \infty } \left( {ax + \sqrt {{x^2} + bx + 1} } \right)\\ = \mathop {\lim }\limits_{x \to  - \infty } \frac{{{a^2}{x^2} - \left( {{x^2} + bx + 1} \right)}}{{ax - \sqrt {{x^2} + bx + 1} }}\\ = \mathop {\lim }\limits_{x \to  - \infty } \frac{{\left( {{a^2} - 1} \right){x^2} - bx - 1}}{{ax - \sqrt {{x^2} + bx + 1} }}\\ = \mathop {\lim }\limits_{x \to  - \infty } \frac{{\left( {{a^2} - 1} \right){x^2} - bx - 1}}{{ax - \left| x \right|\sqrt {1 + \frac{b}{x} + \frac{1}{{{x^2}}}} }}\\ = \mathop {\lim }\limits_{x \to  - \infty } \frac{{\left( {{a^2} - 1} \right){x^2} - bx - 1}}{{ax + x\sqrt {1 + \frac{b}{x} + \frac{1}{{{x^2}}}} }}\\ = \mathop {\lim }\limits_{x \to  - \infty } \frac{{\left( {{a^2} - 1} \right){x^2} - bx - 1}}{{x\left( {a + \sqrt {1 + \frac{b}{x} + \frac{1}{{{x^2}}}} } \right)}}\end{array}\)

Nếu \({a^2} - 1 \ne 0\) và \(a > 0\) thì \(L = \infty \) nên loại.

Do đó \({a^2} = 1 \Leftrightarrow a = 1\) (vì \(a > 0\)). Khi đó,

\(L = \mathop {\lim }\limits_{x \to  - \infty } \frac{{ - bx - 1}}{{x\left( {1 + \sqrt {1 + \frac{b}{x} + \frac{1}{{{x^2}}}} } \right)}}\) \( =  - \frac{b}{2}\)

\( \Rightarrow L = \frac{1}{2} \Leftrightarrow  - \frac{b}{2} = \frac{1}{2}\) \( \Leftrightarrow b =  - 1\).

\( \Rightarrow A = 2a + b = 2.1 + \left( { - 1} \right) = 1\)

Chọn D

Câu 13 (TH):

Phương pháp:

Sử dụng công thức: \({u_n} = {u_1}{q^{n - 1}}\).

Cách giải:

Ta có:

\(\begin{array}{l}q = \frac{{{u_2}}}{{{u_1}}} = \frac{6}{{ - 3}} =  - 2\\ \Rightarrow {u_5} = {u_1}{q^4} = \left( { - 3} \right).{\left( { - 2} \right)^4} =  - 48\end{array}\)

Chọn C

Câu 14 (TH):

Phương pháp:

Tính các giới hạn và kiểm tra.

Cách giải:

Đáp án A và B đều loại vì \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{ - x + 4}}{{x - 1}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{{ - x + 4}}{{x - 1}} =  - 1\).

Đáp án B: Vì \(\mathop {\lim }\limits_{x \to {1^ - }} \left( { - x + 4} \right) = 3 > 0\) và \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ - }} \left( {x - 1} \right) = 0\\x - 1 < 0,\forall x < 1\end{array} \right.\) nên \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{ - x + 4}}{{x - 1}} =  - \infty \)

Chọn C

Câu 15 (TH):

Phương pháp:

Chứng minh \(\left( {AD,SC} \right) = \left( {BC,SC} \right)\) và tính toán.

Cách giải:

Ta có: \(AD//BC\) \( \Rightarrow \left( {AD,SC} \right) = \left( {BC,SC} \right)\)

Ta thấy: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)

Hay tam giác \(SBC\) vuông tại \(B\).

Có \(SB = \sqrt {S{A^2} + A{B^2}} \) \( = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \)

\( \Rightarrow \tan \widehat {SCB} = \frac{{SB}}{{BC}} = \frac{{a\sqrt 2 }}{{a\sqrt 2 }} = 1\) \( \Rightarrow \widehat {SCB} = {45^0}\)

\( \Rightarrow \left( {BC,SC} \right) = \widehat {SCB} = {45^0}\) hay \(\left( {AD,SC} \right) = {45^0}\).

Chọn B

Câu 16 (TH):

Phương pháp:

Rút gọn hàm số đã cho để tính đạo hàm.

Cách giải:

Ta có:

\(\begin{array}{l}y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\\ = \frac{{{x^2} + 2x + 1 + 1}}{{x + 1}}\\ = \frac{{{{\left( {x + 1} \right)}^2} + 1}}{{x + 1}}\\ = x + 1 + \frac{1}{{x + 1}}\\ \Rightarrow y' = 1 - \frac{1}{{{{\left( {x + 1} \right)}^2}}}\\ = \frac{{{{\left( {x + 1} \right)}^2} - 1}}{{{{\left( {x + 1} \right)}^2}}}\\ = \frac{{{x^2} + 2x + 1 - 1}}{{{{\left( {x + 1} \right)}^2}}}\\ = \frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}}\end{array}\)

Chọn D

Câu 17 (TH):

Phương pháp:

Xác định góc giữa các cặp đường thẳng đã cho và kết luận.

Cách giải:

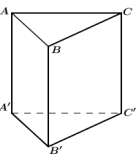
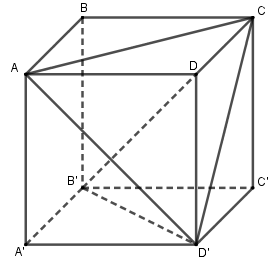
Đáp án A: \(AA'//DD'\) \( \Rightarrow \left( {B'D,AA'} \right) = \left( {B'D,DD'} \right)\) \( = \widehat {B'DD'} < {90^0}\) vì \(\widehat {DD'B'} = {90^0}\).

Do đó A sai.

Đáp án B:

Ta thấy, \(AD' \bot \left( {A'DCB'} \right)\) \( \Rightarrow AD' \bot B'D\) nên B đúng.

Đáp án C:

Lại có, \(AC \bot \left( {BDD'B'} \right)\) \( \Rightarrow AC \bot B'D\)

\(\left\{ \begin{array}{l}B'D \bot AD'\\B'D \bot AC\end{array} \right.\) \( \Rightarrow B'D \bot \left( {ACD'} \right)\) nên C đúng.

Đáp án D: \(AB//A'B'\), mà \(A'B' \bot B'C'\) nên \(AB \bot B'C'\) hay D đúng.

Chọn A

Câu 18 (TH):

Phương pháp:

Tính \(y'\) và sử dụng công thức \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\).

Cách giải:

Ta có: \(y' = 3{x^2} + 6x\).

Với \({x_0} =  - 1\) thì \({y_0} = {\left( { - 1} \right)^3} + 3.{\left( { - 1} \right)^2} - 1 = 1\)

Hệ số góc \(k = y'\left( { - 1} \right)\) \( = 3.{\left( { - 1} \right)^2} + 6.\left( { - 1} \right) =  - 3\)

Phương trình tiếp tuyến: \(y =  - 3\left( {x + 1} \right) + 1\) hay \(y =  - 3x - 2\).

Chọn B

Câu 19 (NB):

Phương pháp:

Dãy số \(\left( {{u_n}} \right)\) là 1 CSC nếu \({u_{n + 1}} = {u_n} + d\) với mọi \(n \in {\mathbb{N}^*}\)

Cách giải:

Quan sát các đáp án ta thấy, chỉ có đáp án D có \({u_{n + 1}} - {u_n} = 2 \Leftrightarrow {u_{n + 1}} = {u_n} + 2\) nên là CSC.

Chọn D

Câu 20 (VD):

Phương pháp:

Gọi M là trung điểm của A’B’, kẻ C’H vuông góc CM.

Chứng minh \(C'H \bot CM\) và tính khoảng cách.

Cách giải:

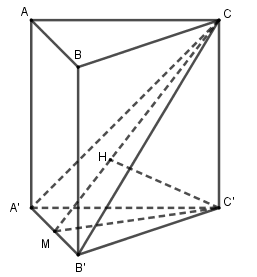
Tam giác \(CA'B'\) cân tại \(C\) vì \(CA' = CB'\) (hai đường chéo của hai hình chữ nhật bằng nhau)

Gọi M là trung điểm của \(A'B'\).

Ta có: \(A'B' \bot CM\) và \(A'B' \bot C'M\) nên \(A'B' \bot \left( {CMC'} \right)\).

Trong \(\left( {CMC'} \right)\), kẻ \(C'H \bot CM\) ta có:

\(\left\{ \begin{array}{l}C'H \bot A'B'\\C'H \bot CM\end{array} \right.\) \( \Rightarrow C'H \bot \left( {CA'B'} \right)\)

\( \Rightarrow d\left( {C',\left( {CA'B'} \right)} \right) = C'H\).

Tam giác \(A'B'C'\) đều cạnh \(a\) nên \(C'M = \frac{{a\sqrt 3 }}{2}\).

Tam giác \(CMC'\) vuông tại \(C'\) nên:

\(\frac{1}{{C'{H^2}}} = \frac{1}{{C'{C^2}}} + \frac{1}{{C'{M^2}}}\)\( = \frac{1}{{{{\left( {\frac{{3a}}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{{16}}{{9{a^2}}}\)

\( \Rightarrow C'{H^2} = \frac{{9{a^2}}}{{16}} \Rightarrow C'H = \frac{{3a}}{4}\)

Vậy \(d\left( {C',\left( {CA'B'} \right)} \right) = \frac{{3a}}{4}\)

Chọn D

PHẦN II: TỰ LUẬN (5 điểm)

Câu 1 (VD):

Phương pháp:

Sử dụng tính chất của cấp số cộng \(\left( {{u_n}} \right)\) là \({u_{k - 1}} + {u_{k + 1}} = 2{u_k}\)

Tính chất cấp số nhân \(\left( {{v_n}} \right)\) là \({v_{k - 1}}.{v_{k + 1}} = v_k^2\)

Cách giải:

Gọi ba số hạng liên tiếp của cấp số cộng là: \(x;y;z\)

Ta có: \(x + z = 2y\) và \(x + y + z = 45\) nên \(3y = 45 \Leftrightarrow y = 15\)

Suy ra \(x + z = 30\)

Theo đề bài, nếu bớt 6 đơn vị ở số hạng thứ hai và giữ nguyên các số còn lại thì được một cấp số nhân nên ta có \(x;9;z\) là một cấp số nhân

Từ đó \(x.z = {9^2}\) \( \Leftrightarrow xz = 81\)

Ta có: \(\left\{ \begin{array}{l}x + z = 30\\xz = 81\end{array} \right.\)  nên \(x;z\) là nghiệm của phương trình \({X^2} - 30X + 81 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}X = 27\\X = 3\end{array} \right.\)

Suy ra \(x = 27;z = 3\) hoặc \(x = 3;z = 27\)

Vậy ba số cần tìm là \(27;15;3\)

Câu 2 (VD):

Phương pháp:

a) Tính \(f'\left( x \right)\) rồi giải bất phương trình \(f'\left( x \right) > 0\)

b) Tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại \(M\left( {{x_0};{y_0}} \right)\) có phương trình \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\)

Chú ý hai đường thẳng song song có cùng hệ số góc

Cách giải:

Ta có: \(f'\left( x \right) = 6{x^2} - 6x + 7\)

a) \(f'\left( x \right) > 0\) \( \Leftrightarrow 6{x^2} - 6x + 7 > 0\)

\(\begin{array}{l} \Leftrightarrow 6\left( {{x^2} - x + \frac{7}{6}} \right) > 0\\ \Leftrightarrow {x^2} - x + \frac{1}{4} + \frac{{11}}{{12}} > 0\end{array}\)

\( \Leftrightarrow {\left( {x - \frac{1}{2}} \right)^2} + \frac{{11}}{{12}} > 0\) (luôn đúng với mọi \(x\))

Vậy bất phương trình \(f'\left( x \right) > 0\) có tập nghiệm \(S = \mathbb{R}\).

b) Vì tiếp tuyến song song với đường thẳng \(y = 7x - 15\) nên hệ số góc của tiếp tuyến \(k = 7\)

Gọi \(M\left( {{x_0};{y_0}} \right)\) là tọa độ tiếp điểm của tiếp tuyến với đồ thị hàm số

Ta có \(f'\left( {{x_0}} \right) = 7\)

\(\begin{array}{l} \Leftrightarrow 6x_0^2 - 6{x_0} + 7 = 7\\ \Leftrightarrow 6x_0^2 - 6{x_0} = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} = 0 \Rightarrow {y_0} =  - 15\\{x_0} = 1 \Rightarrow {y_0} =  - 9\end{array} \right.\end{array}\)

Với \(M\left( {0; - 15} \right)\) ta có phương trình tiếp tuyến \(y = 7\left( {x - 0} \right) - 15\) \( \Leftrightarrow y = 7x - 15\) (loại vì trùng với đường thẳng đã cho)

Với \(M\left( {1; - 9} \right)\) ta có phương trình tiếp tuyến \(y = 7\left( {x - 1} \right) - 9\) \( \Leftrightarrow y = 7x - 16\) (nhận)

Vậy tiếp tuyến cần tìm có phương trình \(y = 7x - 16\)

Câu 3 (VD):

Phương pháp:

a) Chứng minh \(BD \bot \left( {ADC} \right)\) từ đó suy ra \(\left( {SAC} \right) \bot \left( {SBD} \right)\)

b) Góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) là góc giữa \(d\) và \(d'\) với \(d'\) là hình chiếu của đường thẳng \(d\) lên mặt phẳng \(\left( P \right)\)

c) Sử dụng: \(AB \cap \left( P \right) = \left\{ M \right\}\) \( \Rightarrow \frac{{d\left( {A;\left( P \right)} \right)}}{{d\left( {B;\left( P \right)} \right)}} = \frac{{AM}}{{BM}}\)

Từ đó đưa về tính \(d\left( {A;\left( {SMC} \right)} \right) = AH\) với \(AH \bot \left( {SMC} \right)\) tại \(H.\)

Tính toán dựa vào hệ thức lượng trong tam giác vuông

Cách giải:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh \(a\). Hai mặt phẳng \(\left( {SAB} \right),\left( {SAD} \right)\) cùng vuông góc với mặt phẳng đáy, \(SA = 2a\).

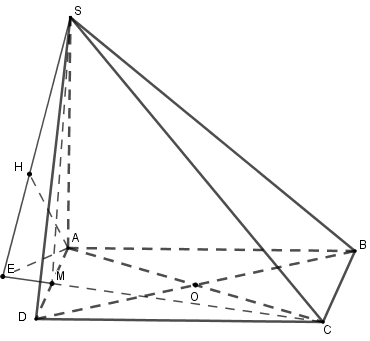
a) Chứng minh rằng \(\left( {SAC} \right) \bot \left( {SBD} \right)\)

Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAD} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {SAD} \right) = SA\end{array} \right.\) \( \Rightarrow SA \bot \left( {ABCD} \right)\) \( \Rightarrow SA \bot BD\)

Vì \(ABCD\) là hình vuông nên \(AC \bot BD\)

Ta có: \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AC\\SA \cap AC = \left\{ A \right\}\end{array} \right.\) \( \Rightarrow BD \bot \left( {SAC} \right)\) mà \(BD \subset \left( {SBD} \right)\) nên \(\left( {SAC} \right) \bot \left( {SBD} \right)\)

b) Xác định và tính tang của góc giữa đường thẳng \(SC\) và \(\left( {ABCD} \right)\).

Vì \(SA \bot \left( {ABCD} \right)\) nên \(AC\) là hình chiếu của \(SC\) lên mặt phẳng \(\left( {ABCD} \right)\)

Suy ra góc giữa \(SC\) và \(\left( {ABCD} \right)\) là góc giữa \(SC\) và \(AC\), hay là góc \(\widehat {SCA}\)

Xét tam giác \(ADC\) vuông tại \(D\) có \(AC = \sqrt {A{D^2} + D{C^2}} \) \( = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \)

Vì \(SA \bot \left( {ABCD} \right)\) \( \Rightarrow SA \bot AC\)

Xét tam giác \(SAC\) vuông tại \(A\) có \(\tan \widehat {SCA} = \frac{{SA}}{{AC}}\) \( = \frac{{2a}}{{a\sqrt 2 }} = \sqrt 2 \)

Vậy góc cần tìm là \(\widehat {SCA}\) và \(\tan \widehat {SCA} = \sqrt 2 .\)

c) Gọi \(M\) là trung điểm của \(AD\). Tính khoảng cách từ điểm \(O\) đến mặt phẳng \(\left( {SMC} \right)\).

Ta có: \(AO \cap \left( {SMC} \right)\) tại \(C\) nên \(\frac{{d\left( {O;\left( {SMC} \right)} \right)}}{{d\left( {A;\left( {SMC} \right)} \right)}}\) \( = \frac{{OC}}{{AC}} = \frac{1}{2}\)\( \Rightarrow d\left( {O;\left( {SMC} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SMC} \right)} \right)\)

Trong \(\left( {ABCD} \right)\) kẻ \(AE \bot CM\) tại \(E\) (vì \(\widehat {MAC} = {45^0};\widehat {ACM} < {45^0}\) nên \(\Delta AMC\) là tam giác tù nên \(E\) nằm ngoài đoạn \(MC\))

Ta có: \(\left\{ \begin{array}{l}SA \bot \left( {ABCD} \right)\\CM \subset \left( {ABCD} \right)\end{array} \right.\)  nên \(SA \bot CM\)

Do đó \(\left\{ \begin{array}{l}CM \bot AE\\CM \bot SA\\SA \cap AE = \left\{ A \right\}\end{array} \right.\) \( \Rightarrow CM \bot \left( {SAE} \right)\) mà \(CM \subset \left( {SMC} \right)\) nên \(\left( {SAE} \right) \bot \left( {SMC} \right)\)

Trong \(\left( {SAE} \right)\) kẻ \(AH \bot SE\) tại \(E\) . Ta có:

\(\left\{ \begin{array}{l}\left( {SAE} \right) \bot \left( {SMC} \right)\\\left( {SAE} \right) \cap \left( {SMC} \right) = SE\\AH \bot SE = \left\{ H \right\}\\AH \subset \left( {SAE} \right)\end{array} \right.\) \( \Rightarrow AH \bot \left( {SMC} \right)\) tại \(H\)

Suy ra \(d\left( {A;\left( {SMC} \right)} \right) = AH\)

Xét tam giác \(ADC\) vuông tại D nên \({S_{ADC}} = \frac{1}{2}AD.DC = \frac{1}{2}{a^2}\)

Mà \(M\) là trung điểm \(AD\) nên \({S_{AMC}} = \frac{1}{2}{S_{ADC}}\) \( = \frac{1}{4}{a^2}\)

Xét tam giác \(MDC\) vuông tại \(D\) có \(MD = \frac{a}{2};DC = a\) nên \(MC = \sqrt {M{D^2} + D{C^2}} \) \( = \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {a^2}}  = \frac{{a\sqrt 5 }}{2}\)

Lại có \({S_{AMC}} = \frac{1}{2}AE.MC\) \( \Leftrightarrow AE = \frac{{2{S_{AMC}}}}{{MC}}\) \( = \frac{{2.\frac{{{a^2}}}{4}}}{{\frac{{a\sqrt 5 }}{2}}} = \frac{a}{{\sqrt 5 }}\)

Vì \(\left\{ \begin{array}{l}SA \bot \left( {ABCD} \right)\\AE \subset \left( {ABCD} \right)\end{array} \right.\) nên \(SA \bot AE\)

Xét tam giác vuông \(SAE\) có \(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{E^2}}}\) \( = \frac{1}{{{{\left( {2a} \right)}^2}}} + \frac{1}{{{{\left( {\frac{a}{{\sqrt 5 }}} \right)}^2}}}\) \( = \frac{{21}}{{4{a^2}}}\)

\( \Rightarrow AH = \frac{{2\sqrt {21} }}{{21}}a\)

Do đó  \(d\left( {O;\left( {SMC} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SMC} \right)} \right)\)\( = \frac{1}{2}.\frac{{2\sqrt {21} }}{{21}}a = \frac{{\sqrt {21} }}{{21}}a\)

Vậy \(d\left( {O;\left( {SMC} \right)} \right) = \frac{{\sqrt {21} }}{{21}}a\).

Loigiaihay.com