Giải câu hỏi trắc nghiệm trang 69, 70 sách bài tập toán 9 - Kết nối tri thức tập 1Trong mặt phẳng tọa độ Oxy, cho đường tròn (O; (sqrt 5 )), hai điểm (Aleft( { - sqrt 3 ;1} right)) và B(-1; 2). Khi đó xảy ra: A. Điểm A nằm trong (O), điểm B nằm ngoài (O). B. Điểm A nằm trong (O), điểm B nằm trên (O). C. Điểm A nằm trên (O), điểm B nằm trong (O). D. Điểm A nằm ngoài (O), điểm B nằm trên (O). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
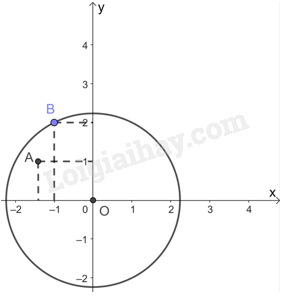
Câu 1 Trả lời câu hỏi Câu 1 trang 69, 70 SBT Toán 9 Kết nối tri thức Trong mặt phẳng tọa độ Oxy, cho đường tròn (O; \(\sqrt 5 \)), hai điểm \(A\left( { - \sqrt 3 ;1} \right)\) và B(-1; 2). Khi đó xảy ra: A. Điểm A nằm trong (O), điểm B nằm ngoài (O). B. Điểm A nằm trong (O), điểm B nằm trên (O). C. Điểm A nằm trên (O), điểm B nằm trong (O). D. Điểm A nằm ngoài (O), điểm B nằm trên (O). Phương pháp giải: Biểu diễn đường tròn (O; \(\sqrt 5 \)), hai điểm \(A\left( { - \sqrt 3 ;1} \right)\) và B(-1; 2) trên mặt phẳng tọa độ Oxy, từ đó rút ra kết luận. Lời giải chi tiết:
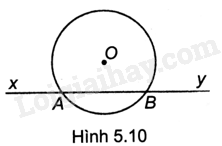
Từ hình vẽ trên, ta thấy điểm A nằm trong (O), điểm B nằm trên (O). Chọn B Câu 2 Trả lời câu hỏi Câu 2 trang 70 SBT Toán 9 Kết nối tri thức Cho đường thẳng xy cắt đường tròn (O) tại hai điểm A và B (H.5.10). Khi đó, các điểm thuộc đường thẳng xy và nằm trong đường tròn (O) là:
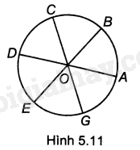
A. Các điểm thuộc tia AB. B. Các điểm thuộc tia By. C. Các điểm thuộc đoạn AB. D. Các điểm nằm giữa A và B. Phương pháp giải: Nhìn hình vẽ và đưa ra kết luận. Lời giải chi tiết: Từ hình vẽ ta thấy, các điểm thuộc đường thẳng xy và nằm trong đường tròn (O) là các điểm nằm giữa A và B. Chọn D Câu 3 Trả lời câu hỏi Câu 3 trang 70 SBT Toán 9 Kết nối tri thức Cho Hình 5.11, trong đó tất cả các cung AB, BC, CD, DE, EG và GA đều có số đo bằng \({60^o}\). Khi đó:
A. Điểm đối xứng với A qua CG là B. B. Điểm đối xứng với A qua CG là D. C. Điểm đối xứng với A qua CG là E. D. Điểm đối xứng với A qua CG là G. Phương pháp giải: + Chứng minh OG là tia phân giác của góc EOA. + Chứng minh tam giác EOA cân tại O. Do đó, OG là đường phân giác đồng thời là đường trung trực của AE. Suy ra điểm đối xứng với A qua CG là E. Lời giải chi tiết: Vì sđ$\overset\frown{EG}$=sđ$\overset\frown{GA}$ nên \(\widehat {EOG} = \widehat {GOA}\). Do đó, OG là tia phân giác của góc EOA. Tam giác EOA có: \(OA = OE\) nên tam giác EOA cân tại O. Do đó, OG là đường phân giác đồng thời là đường trung trực của tam giác EOA. Suy ra, OG là đường trung trực của đoạn thẳng AE. Vậy điểm đối xứng với A qua CG là E. Chọn C Câu 4 Trả lời câu hỏi Câu 4 trang 70 SBT Toán 9 Kết nối tri thức Độ dài L (đơn vị cm) của cung tròn và diện tích S của hình quạt tròn (đơn vị \(c{m^2}\)) có cùng bán kính 9cm và cùng ứng với cung \({280^o}\) là: A. \(L = 7\pi \) và \(S = 63\pi \). B. \(L = 14\pi \) và \(S = 63\pi \). C. \(L = 7\pi \) và \(S = 28\pi \). D. \(L = 14\pi \) và \(S = 28\pi \). Phương pháp giải: Độ dài l của cung \({n^o}\) trên đường tròn (O; R) là \(l = \frac{n}{{180}}.\pi R\). Diện tích \({S_q}\) của hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{n}{{360}}.\pi {R^2}\). Lời giải chi tiết: Độ dài L của cung \({280^o}\) bán kính 9cm là \(L = \frac{{280}}{{180}}.\pi .9 = 14\pi \left( {cm} \right)\). Diện tích \({S_q}\) của hình quạt tròn bán kính 9cm ứng với cung \({280^o}\): \({S_q} = \frac{{280}}{{360}}.\pi {.9^2} = 63\pi \left( {c{m^2}} \right)\). Chọn B Câu 5 Trả lời câu hỏi Câu 5 trang 70 SBT Toán 9 Kết nối tri thức Cho góc nhọn xOy và điểm M nằm trong góc đó. Biết rằng M nằm cách Ox một khoảng bằng 3cm và cách Oy một khoảng bằng 2cm. Khi đó A. Nếu đường tròn (M) tiếp xúc với Ox thì (M) cắt Oy. B. Nếu đường tròn (M) tiếp xúc với Ox thì (M) cũng tiếp xúc với Oy. C. Nếu đường tròn (M) tiếp xúc với Ox thì (M) không giao nhau với Oy. D. Nếu đường tròn (M) tiếp xúc với Oy thì (M) cắt Ox. Phương pháp giải: Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Khi đó: + Đường thẳng a và đường tròn (O; R) cắt nhau khi \(d < R\). + Đường thẳng a và đường tròn (O; R) tiếp xúc với nhau khi \(d = R\). + Đường thẳng a và đường tròn (O; R) không giao nhau khi \(d > R\). Lời giải chi tiết: Gọi A và B lần lượt là giao điểm của đường thẳng qua M vuông góc Ox và Oy. Khi đó, MA và MB lần lượt là khoảng cách từ điểm M đến trục Ox và Oy. Do đó: \(MA = 3cm,MB = 2cm\). Nếu đường tròn (M) tiếp xúc với Ox thì bán kính của (M) là \(MA = 3cm\). Vì \(MA > MB\left( {do\;3cm > 2cm} \right)\) nên đường tròn (M) cắt trục Oy. Vậy nếu đường tròn (M) tiếp xúc với Ox thì (M) cắt Oy. Chọn A Câu 6 Trả lời câu hỏi Câu 6 trang 70 SBT Toán 9 Kết nối tri thức Cho hai điểm A và B sao cho \(AB = 7cm\) và đường tròn (B; 4cm). Khi đó: A. Hai đường tròn (A; R) và (B) cắt nhau nếu \(R < 11cm\). B. Hai đường tròn (A; R) và (B) cắt nhau nếu \(R > 3cm\). C. Hai đường tròn (A; R) và (B) không giao nhau nếu \(R > 11cm\). D. Hai đường tròn (A; R) và (B) không giao nhau nếu \(R \le 3cm\). Phương pháp giải: Hai đường tròn (O; R) và (O’; r) (với \(R > r\)). Khi đó: + Hai đường tròn ở ngoài nhau khi \(OO' > R + r\). + Hai đường tròn tiếp xúc ngoài khi \(OO' = R + r\). + Hai đường tròn cắt nhau khi \(R - r < OO' < R + r\). + Hai đường tròn tiếp xúc trong khi \(OO' = R - r\). + Đường tròn (O) đựng (O’) khi \(OO' < R - r\). Lời giải chi tiết: Hai đường tròn (A; R) và (B) cắt nhau khi \(\left| {R - 4} \right| < 7 < 4 + R\) Với \(4 + R > 7\), suy ra \(R > 3\) Với \(\left| {R - 4} \right| < 7\) thì \( - 7 < R - 4 < 7\), suy ra \( - 3 < R < 11\). Vậy hai đường tròn (A; R) và (B) cắt nhau khi \(3 < R < 11\) Hai đường tròn (A; R) và (B) không giao nhau khi \(4 + R < 7\) hoặc \(\left| {R - 4} \right| > 7\). Suy ra \(R < 3\) hoặc \(R > 11\). Chọn C
|




















Danh sách bình luận