Giải bài tập 1.31 trang 45 SGK Toán 12 tập 1 - Cùng khám pháTừ một miếng bìa hình chữ nhật với kích thước 20cm x 10cm, bạn Lan cắt bỏ hai hình vuông có cạnh là x (cm) và hai hình chữ nhật (phần gạch sọc Hình 1.65) rồi gấp theo đường nét đứt và dán các mép để được một cái hộp có dạng hình hộp chữ nhật. Tìm x để thể tích hộp là lớn nhất và tính giá trị lớn nhất đó. Quảng cáo
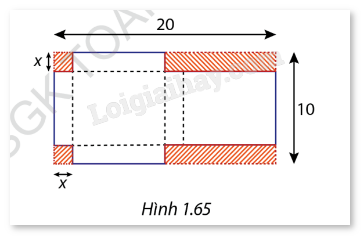
Đề bài Từ một miếng bìa hình chữ nhật với kích thước 20cm x 10cm, bạn Lan cắt bỏ hai hình vuông có cạnh là x (cm) và hai hình chữ nhật (phần gạch sọc Hình 1.65) rồi gấp theo đường nét đứt và dán các mép để được một cái hộp có dạng hình hộp chữ nhật. Tìm x để thể tích hộp là lớn nhất và tính giá trị lớn nhất đó.
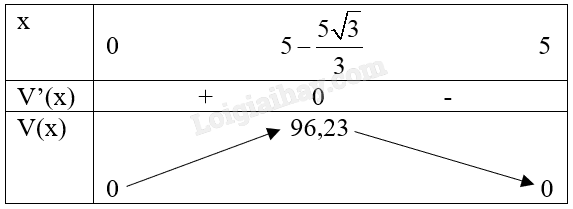
Phương pháp giải - Xem chi tiết - Xác định chiều dài, chiều rộng và chiều cao của hộp sau khi cắt bỏ hình vuông và hình chữ nhật. - Tìm công thức của hộp dựa trên các kích thước đã được xác định. - Khảo sát hàm số thể tích để tìm giá trị lớn nhất. Lời giải chi tiết - Sau khi cắt bỏ và gấp lại, các phần còn lại của miếng bìa sẽ tạo thành một hình hộp chữ nhật kích thước: Chiều dài: \(\frac{{20}}{2} - x = 10 - x\) (cm) Chiều rộng: 10−2𝑥 (cm) Chiều cao: 𝑥 (cm) - Thể tích của hình hộp chữ nhật là: \(\begin{array}{l}V = x.(10 - x).(10 - 2x)\\ = (10x - {x^2}).(10 - 2x)\\ = 2{x^3} - 30{x^2} + 100x\end{array}\) - Đạo hàm của hàm số thể tích là: \(V'(x) = 6{x^2} - 60x + 100\) - Giải phương trình \(V'(x) = 0\): \(6{x^2} - 60x + 100 = 0 \Leftrightarrow 3{x^2} - 30x + 50 = 0 \Rightarrow x = 5 \pm \frac{{5\sqrt 3 }}{5}\) Vì miền xác định của 𝑥 là \(0 \le x \le 5\)nên chỉ nhận giá trị \(x = 5 - \frac{{5\sqrt 3 }}{5}\) - Bảng biến thiên:
Vậy \(x = 5 - \frac{{5\sqrt 3 }}{5} \approx 2,11\) thì thể tích hình hộp là lớn nhất và có giá trị là \({V_{\max }} \approx 96.23\)cm3.  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
