Giải bài 9.42 trang 60 sách bài tập toán 9 - Kết nối tri thức tập 2

Đề bài

Một phép quay thuận chiều \({120^o}\) tâm O biến điểm A thành điểm B, biến điểm B thành điểm C. Chứng tỏ rằng tam giác ABC là tam giác đều nội tiếp một đường tròn tâm O.

Lời giải chi tiết

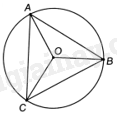
Ta có: \(OA = OB = OC\) nên tam giác ABC nội tiếp (O) và các cung nhỏ AB, BC có số đo bằng \({120^o}\).

Vì góc ACB và góc BAC là các góc nội tiếp đường tròn (O) lần lượt chắn các cung nhỏ AB, BC nên \(\widehat {ACB} = \frac{1}{2}\)sđ$\overset\frown{AB}$_nhỏ\( = {60^o}\), \(\widehat {BAC} = \frac{1}{2}\)sđ$\overset\frown{BC}$ _nhỏ \( = {60^o}\).

Tam giác ABC có: \(\widehat {ABC} = {180^o} - \widehat {ACB} - \widehat {BAC} = {60^o}\).

Tam giác ABC có: \(\widehat {ABC} = \widehat {ACB} = \widehat {CAB} = {60^o}\) nên tam giác ABC đều.