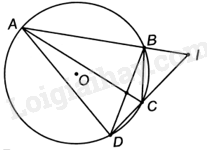
Giải bài 9.25 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 2Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai tia AB và DC cắt nhau tại điểm I. Chứng minh rằng: a) $Delta IADbacksim Delta ICB,Delta IACbacksim Delta IDB$; b) (frac{{IC}}{{ID}} = frac{{AC}}{{AD}}.frac{{BC}}{{BD}}). Quảng cáo
Đề bài Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai tia AB và DC cắt nhau tại điểm I. Chứng minh rằng: a) $\Delta IAD\backsim \Delta ICB,\Delta IAC\backsim \Delta IDB$; b) \(\frac{{IC}}{{ID}} = \frac{{AC}}{{AD}}.\frac{{BC}}{{BD}}\). Phương pháp giải - Xem chi tiết a) + Chứng minh \(\widehat {IAD} = \widehat {ICB}\), từ đó chứng minh được $\Delta IAD\backsim \Delta ICB\left( g.g \right)$. + Chứng minh \(\widehat {IAC} = \widehat {IDB}\), từ đó chứng minh được $\Delta IAC\backsim \Delta IDB\left( g.g \right)$. b) Từ a ta suy ra: \(\frac{{IC}}{{IA}} = \frac{{BC}}{{AD}}\), \(\frac{{IA}}{{ID}} = \frac{{AC}}{{BD}}\). Do đó, \(\frac{{IC}}{{ID}} = \frac{{IC}}{{IA}}.\frac{{IA}}{{ID}} = \frac{{AC}}{{AD}}.\frac{{BC}}{{BD}}\). Lời giải chi tiết
a) Vì tứ giác ABCD nội tiếp (O) nên \(\widehat {IAD} + \widehat {BCD} = {180^o}\). Mà \(\widehat {ICB} + \widehat {BCD} = {180^o}\) nên \(\widehat {IAD} = \widehat {ICB}\). Tam giác IAD và tam giác ICB có: góc I chung, \(\widehat {IAD} = \widehat {ICB}\) nên $\Delta IAD\backsim \Delta ICB\left( g.g \right)$. Tam giác IAC và tam giác IDB có: góc I chung, \(\widehat {IAC} = \widehat {IDB}\) (hai góc nội tiếp (O) cùng chắn cung BC) Do đó, $\Delta IAC\backsim \Delta IDB\left( g.g \right)$. b) Vì $\Delta IAD\backsim \Delta ICB$ nên \(\frac{{IC}}{{IA}} = \frac{{BC}}{{AD}}\); $\Delta IAC\backsim \Delta IDB$ nên \(\frac{{IA}}{{ID}} = \frac{{AC}}{{BD}}\). Do đó, \(\frac{{IC}}{{ID}} = \frac{{IC}}{{IA}}.\frac{{IA}}{{ID}} = \frac{{AC}}{{AD}}.\frac{{BC}}{{BD}}\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
