Giải Bài 9.23 trang 60 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

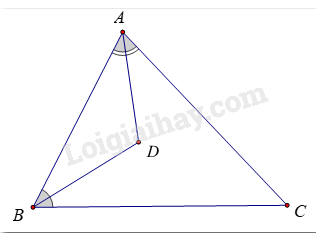
Đề bài

Cho D là một điểm bên trong tam giác ABC. Chứng minh:

a)\(\widehat {BDC} > \widehat {BAC}\)

b) BD + DC < AB + AC

Lời giải chi tiết

a)

 

Tia AD chia góc A thành góc A₁ và góc A₂, chia góc BDC thành góc D₁ và góc D₂.

Góc D₁ là góc ngoài tại đỉnh D của tam giác ABD nên:

\(\widehat {{D_1}} > \widehat {{A_1}}\)

Góc D₂ là góc ngoài tại đỉnh D của tam giác ADC nên:

\(\widehat {{D_2}} > \widehat {{A_2}}\)

\( \Rightarrow \widehat D = \widehat {{D_1}} + \widehat {{D_2}} > \widehat {{A_1}} + \widehat {{A_2}} = \widehat A\)

b)

Gọi E là giao điểm của BD và AC. Ta có:

AB + AC = AB + (AE + EC) = (AB + AE) + EC

Mà: AB + AE > BE (bất đẳng thức trong tam giác ABE)

=>(AB + AE) + EC > BE + EC = (BD + DE) + EC = BD + (DE + EC)

Mà DE + EC > DC (bất đẳng thức trong tam giác DEC)

=>AB + AC > BD + DC.