Giải Bài 9.13 trang 52 sách bài tập toán 7 - Kết nối tri thức với cuộc sốnga) Cho P là một điểm bên trong tam giác ABC. Chứng minh rằng: AB + AC > PB + PC Quảng cáo
Đề bài a) Cho P là một điểm bên trong tam giác ABC. Chứng minh rằng: AB + AC > PB + PC b) Cho M là một điểm bên trong tam giác ABC. Chứng minh rằng: \(\dfrac{1}{2}\left( {AB + BC + CA} \right) < MA + MB + MC < AB + BC + CA\) Phương pháp giải - Xem chi tiết a) - AB + AC = AB + AN + NC = (AB + AN) + NC -Áp dụng các bất đẳng thức tam giác: tam giác ABN, tam giác PNC. b) -Chứng minh: \(MA + MB + MC > \dfrac{{AB + BC + CA}}{2}\)(áp dụng bđt tam giác ABM, MBC, MAC) -Chứng minh: M là điểm nằm trong tam giác ABC: AB + AC > MB + MC CA + CB > MA + MB BA + BC > MA + MC Lời giải chi tiết
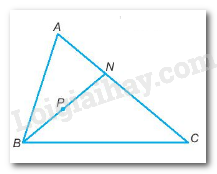
a) P là điểm nằm trong tam giác ABC, đường thẳng BP cắt cạnh AC tại N Ta có: AB + AC = AB + AN + NC = (AB + AN) + NC (1) Xét tam giác ABN: AB + AN > BN (Bất đẳng thức tam giác) =>AB + AN > BP + PN (2) Từ (1) và (2) suy ra: AB + AC > BP + (PN + NC) > BP + PC (Bất đẳng thức tam giác PNC) b) Ta có: MA + MB > AB (bất đẳng thức trong tam giác ABM) MB + MC > BC (bất đẳng thức trong tam giác MBC) MC + MA > CA (bất đẳng thức trong tam giác MAC) Cộng vế trái với vế trái, vế phải với vế phải: 2(MA + MB + MC) > AB + BC + CA Mặt khác theo a) M là điểm nằm trong tam giác ABC: AB + AC > MB + MC CA + CB > MA + MB BA + BC > MA + MC Cộng VT với VT, VP với VP: 2(AB + BC + CA) > 2(MA + MB + MC) =>AB + BC + CA > MA + MB + MC (2) Từ (1) và (2) suy ra: \(\dfrac{1}{2}\left( {AB + BC + CA} \right) < MA + MB + MC < AB + BC + CA\)
|




















Danh sách bình luận