Giải Bài 7 trang 104 sách bài tập toán 7 tập 1 - Cánh diều

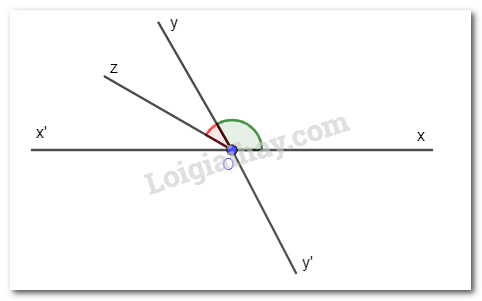
Đề bài

Quan sát Hình 12. Cho hai góc xOy, yOz là hai góc kề nhau, \(\widehat {xOz} = 150^\circ \) và \(\widehat {xOy} - \widehat {yOz} = 90^\circ \).

a) Tính số đo mỗi góc xOy, yOz.

b) Vẽ các tia Ox’ và Oy’ lần lượt là tia đối của các tia Ox, Oy. Tính số đo mỗi góc x’Oy’, y’Oz, xOy’.

 

Lời giải chi tiết

a) Do hai góc xOy, yOz là hai góc kề nhau nên \(\widehat {xOz}=\widehat {xOy} + \widehat {yOz}\). Mà \(\widehat {xOz} = 150^\circ \) nên \(\widehat {xOy} + \widehat {yOz} = 150^\circ \).

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}\widehat {xOy} - \widehat {yOz} = 90^\circ \\\widehat {xOy} + \widehat {yOz} = 150^\circ \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\widehat {xOy} = 120^\circ \\\widehat {yOz} = 30^\circ \end{array} \right.\end{array}\)

Vậy \(\left\{ \begin{array}{l}\widehat {xOy} = 120^\circ \\\widehat {yOz} = 30^\circ \end{array} \right.\).

b)

 

Ta có: \(\widehat {x'Oy'} = \widehat {xOy} = 120^\circ \) (đối đỉnh).

Ta có: \(\widehat {y'Oz} + \widehat {yOz} = 180^\circ \) (hai góc kề bù). Suy ra: \(\widehat {y'Oz} = 180^\circ  - \widehat {yOz} = 180^\circ  - 30^\circ  = 150^\circ \).

Tương tự, ta có: \(\widehat {xOy'} = 180^\circ  - \widehat {xOy} = 180^\circ  - 120^\circ  = 60^\circ \).