Giải Bài 66 trang 88 sách bài tập toán 7 - Cánh diều

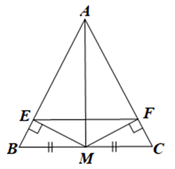
Đề bài

Cho tam giác ABC cân tại A có M là trung điểm BC; ME vuông góc với AB tại E, MF vuông góc với AC tại F. Chứng minh:

a) AM là trung trực của đoạn thẳng BC;

b) ME = MF và AM là đường trung trực của đoạn thẳng EF.

Lời giải chi tiết

 

a) Tam giác ABC cân tại A nên AB = AC (hai cạnh bên).

Suy ra A thuộc đường trung trực của BC.

Lại có M là trung điểm của BC.

Nên AM là đường trung trực của BC.

Vậy AM là trung trực của đoạn thẳng BC.

b) Vì tam giác ABC cân tại A nên \(\hat B = \hat C\) (hai góc ở đáy).

Xét ∆EBM và ∆FCM có:

\(\widehat {BEM} = \widehat {CFM}\left( { = 90^\circ } \right)\)

BM = CM (do M là trung điểm của BC),

\(\hat B = \hat C\) (chứng minh trên)

Do đó ∆EBM = ∆FCM (cạnh huyền – góc nhọn).

Suy ra ME = MF, BE = CF (các cặp cạnh tương ứng).

Do đó M thuộc đường trung trực của EF (1)

Ta có AB = AE + EB, AC = AF + FC.

Mà AB = AC, BE = CF nên AE = AF.

Suy ra A thuộc đường trung trực của EF (2)

Từ (1) và (2) suy ra AM là đường trung trực của EF.

Vậy ME = MF và AM là đường trung trực của EF.