Giải bài 6 trang 89 sách bài tập toán 8 - Cánh diều

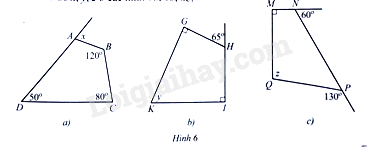
Đề bài

Tính các số đo \(x,y,z\) ở các hình \(6a,6b,6c\):

 

Lời giải chi tiết

a)     Trong tứ giác \(ABCD\), ta có: \(\widehat {DAB} + \widehat B + \widehat C + \widehat D = 360^\circ \).

Do đó: \(\widehat {DAB} = 360^\circ  - \left( {\widehat B + \widehat C + \widehat D} \right) = 360^\circ  - \left( {120^\circ  + 80^\circ  + 50^\circ } \right) = 110^\circ \)

Ta có: \(\widehat {DAB} + x = 180^\circ \) (hai góc kề bù)

Suy ra \(x = 180^\circ  - 110^\circ  = 70^\circ \)

b)    Ta có: \(\widehat {GHI} + 65^\circ  = 180^\circ \) (hai góc kề bù). Suy ra \(\widehat {GHI} = 115^\circ \)

Trong tứ giác \(GHIK\), ta có: \(\widehat G + \widehat {GHI} + \widehat I + \widehat K = 360^\circ \)

Do đó: \(90^\circ  + 115^\circ  + 90^\circ  + y = 360^\circ \) hay \(y + 295^\circ  = 360^\circ \). Suy ra \(y = 65^\circ \)

c)     Ta có: \(\widehat {MNP} + 60^\circ  = 180^\circ \) (hai góc kề bù). Suy ra \(\widehat {MNP} = 120^\circ \)

Ta lại có: \(\widehat {NPQ} + 130^\circ  = 180^\circ \) (hai góc kề bù). Suy ra \(\widehat {NPQ} = 50^\circ \)

Trong tứ giác \(MNPQ\), ta có: \(\widehat M + \widehat {MNP} + \widehat {NPQ} + \widehat Q = 360^\circ \)

Do đó \(90^\circ  + 120^\circ  + 50^\circ  + z = 360^\circ \) hay \(z + 260^\circ  = 360^\circ \). Suy ra \(z = 100^\circ \).