Giải bài 6 trang 104 vở thực hành Toán 8 tập 2

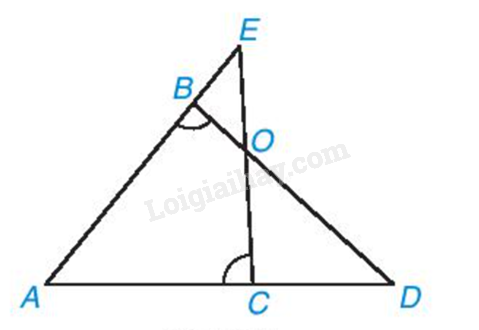
Đề bài

Cho hình 9.25, biết rằng \(\widehat{AB\text{D}}=\widehat{AC\text{E}}\). Chứng minh rằng ΔABD ∽ ΔACE và ΔBOE ∽ ΔCOD.

Lời giải chi tiết

Hai tam giác ABD và ACE có: $\widehat{ABD}=\widehat{ACE}$ (theo giả thiết); góc A chung.

Do đó $\Delta ABD\backsim \Delta ACE$ (g.g).

Hai tam giác BOE và COD có: $\widehat{BOE}=\widehat{COD}$ (hai góc đối đỉnh);

$\widehat{OBE}={{180}^{0}}-\widehat{ABD}={{180}^{0}}-\widehat{ACE}=\widehat{OCD}$.

Do đó $\Delta BOE\backsim \Delta COD$ (g.g).