Giải bài 5.6 trang 59 sách bài tập toán 9 - Kết nối tri thức tập 1

Đề bài

Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Chứng minh rằng:

a) Bốn điểm A, E, H, D cùng thuộc một đường tròn.

b) \(AH > DE\).

Lời giải chi tiết

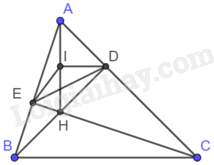
a) Gọi I là trung điểm của AH.

Vì BD và CE là hai đường cao của tam giác ABC nên \(BD \bot AC\) tại D, \(CE \bot AB\) tại E.

Do đó, tam giác AEH vuông tại E và tam giác ADH vuông tại D.

Tam giác AEH vuông tại E, có EI là đường trung tuyến nên \(IA = IE = IH = \frac{1}{2}AH\left( 1 \right)\)

Tam giác ADH vuông tại D, có DI là đường trung tuyến nên \(IA = ID = IH = \frac{1}{2}AH\left( 2 \right)\)

Từ (1) và (2) ta có: \(IA = ID = IH = IE = \frac{1}{2}AH\). Do đó, bốn điểm A, E, H, D cùng thuộc đường tròn tâm I đường kính AH.

b) Vì góc EAD là góc nhọn nên dây DE là dây không đi qua tâm của đường tròn đường kính AH nên \(AH > DE\).