Bài 52 trang 131 Vở bài tập toán 8 tập 1Giải bài 52 trang 131 vở bài tập toán 8 tập 1. Chứng minh rằng: a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Chứng minh rằng: LG a Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi. Phương pháp giải: Áp dụng: +) Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó. Giải chi tiết:
Hình bình hành có tâm đối xứng là giao điểm hai đường chéo. Hình thoi cũng là một hình bình hành, do đó tâm đối xứng của hình thoi cũng là giao điểm hai đường chéo hình thoi. LG b Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi. Phương pháp giải: Áp dụng: +) Hai điểm \(A\) và \(A'\) gọi là đối xứng nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của \(AA'\). Giải chi tiết:
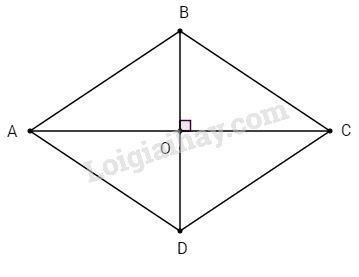
Xét hình thoi \(ABCD\) \(BD\) là đường trung trực của \(AC\) nên \(A\) đối xứng với \(C\) qua \(BD.\) Ta có \(BD\) là trục đối xứng của hình thoi vì \(A\) đối xứng với \(C\) qua \(BD\), \(B\) đối xứng với chính nó qua \(BD,\) \(D\) đối xứng với chính nó qua \(BD.\) Chứng minh tương tự, \(AC\) cũng là trục đối xứng của hình thoi. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
