Bài 49 trang 130 Vở bài tập toán 8 tập 1

Đề bài

Hai đường chéo của một hình thoi bằng \(8cm\) và \(10cm\). Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:

(A) \(6cm\);                     (B) \(\sqrt {41} cm\)

(C) \(\sqrt {164} cm\)               (D) \(9cm\)

Lời giải chi tiết

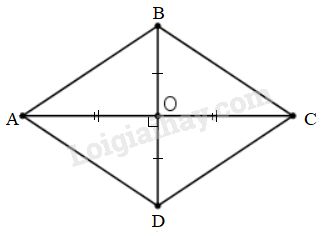
Xét hình thoi \(ABCD\) có \(BD=8\,cm,\)\(AC=10\,cm\).

gọi \(O\) là giao điểm của hai đường chéo. 

Theo tính chất đường chéo hình thoi ta có:

\(AC\bot BD, OA=OC=\dfrac{{AC}}{2} = \dfrac{{10}}{2}\)\(\, = 5\,\,cm,\)

\(OB=OD=\dfrac{{BD}}{2} = \dfrac{8}{2} = 4\,\,cm\)

Áp dụng định lí Pytago vào tam giác \(ABO\) vuông tại \(O\) ta có:

\(A{B^2} = O{A^2} + O{B^2}= {5^2}+{4^2}=41\) nên \(AB =  \sqrt {41} \,cm \).

Vậy câu trả lời (B) là đúng.

Loigiaihay.com