Giải bài 5 trang 82 SGK Toán 8 – Cánh diều

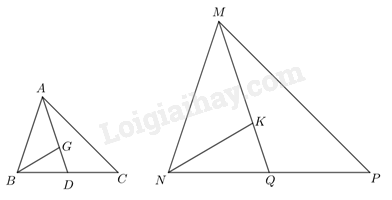
Đề bài

Cho \(\Delta ABC \backsim \Delta MNP\).

a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh \(\Delta ABD \backsim \Delta MNQ\).

b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh \(\Delta ABG \backsim \Delta MNK\).

Lời giải chi tiết

a) Ta có: \(\Delta ABC \backsim \Delta MNP\) suy ra \(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\,\,\left( 1 \right)\) và \(\widehat B = \widehat N\)

Mà D là trung điểm BC và Q là trung điểm NP nên \(BC = 2BD\) và \(NP = 2NQ\)

Thay vào biểu thức (1) ta được \(\frac{{AB}}{{MN}} = \frac{{2BD}}{{2NQ}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\)

Xét tam giác ABD và tam giác MNQ có:

\(\frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\) và \(\widehat B = \widehat N\)

\( \Rightarrow \Delta ABD \backsim \Delta MNQ\) (c-g-c)

b) Vì \(\Delta ABD \backsim \Delta MNQ\) nên ta có \(\frac{{AB}}{{MN}} = \frac{{AD}}{{MQ}}\,\,\left( 2 \right)\) và \(\widehat {BAD} = \widehat {NMQ}\) hay \(\widehat {BAG} = \widehat {NMK}\)

Mà G và K lần lượt là trọng tâm của tam giác ABC và tam giác MNP nên \(AD = \frac{3}{2}AG\) và \(MQ = \frac{3}{2}MK\).

Thay vào (2) ta được: \(\frac{{AB}}{{MN}} = \frac{{\frac{3}{2}AG}}{{\frac{3}{2}MK}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\)

Xét tam giác ABG và tam giác NMK có:

\(\frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\) và \(\widehat {BAG} = \widehat {NMK}\)

\( \Rightarrow \)\(\Delta ABG \backsim \Delta MNK\) (c-g-c)