Giải bài 5 trang 45 sách bài tập toán 8 - Chân trời sáng tạo tập 2Cho tam giác ABC có M, N lần lượt là trung điểm của AC, BC. a) Chứng minh tứ giác AMNB là hình thang. Quảng cáo
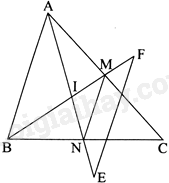
Đề bài Cho tam giác ABC có M, N lần lượt là trung điểm của AC, BC. a) Chứng minh tứ giác AMNB là hình thang. b) Gọi I là giao điểm của AN và BM. Trên tia đối của tia NA lấy điểm E sao cho \(NE = NI\). Trên tia đối của tia MB lấy điểm F sao cho \(MF = MI\). Chứng minh EF//AB. Phương pháp giải - Xem chi tiết + Sử dụng kiến thức về đường trung bình của tam giác để chứng minh: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba. + Sử dụng kiến thức về tính chất của đường trung bình của tam giác để chứng minh: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy. Lời giải chi tiết
a) Xét tam giác ABC có: \(MA = MC,NB = NC\) nên MN là đường trung bình của tam giác ABC, suy ra MN//AB, suy ra tứ giác AMNB là hình thang. b) Xét tam giác IEF có: \(NE = NI\), \(MF = MI\) nên MN là đường trung bình của tam giác EIF, suy ra MN//EF Mà MN//AB, suy ra EF//AB.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
