Giải bài 4.62 trang 70 sách bài tập toán 10 - Kết nối tri thức với cuộc sốngCho hình bình hành ABCD. Gọi M,N theo thứ tự là trung điểm các cạnh AB,CD. Lấy P thuộc đoạn DM và Q thuộc đoạn BN sao cho DP = 2PM,BQ = xQN. Tổng hợp đề thi giữa kì 2 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
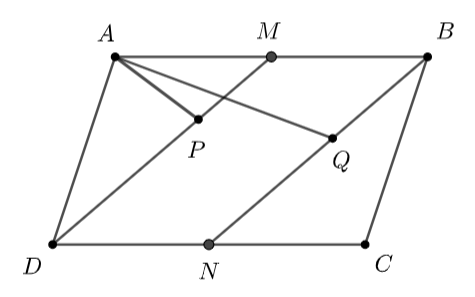
Đề bài Cho hình bình hành \(ABCD.\) Gọi \(M,\,\,N\) theo thứ tự là trung điểm các cạnh \(AB,\,\,CD.\) Lấy \(P\) thuộc đoạn \(DM\) và \(Q\) thuộc đoạn \(BN\) sao cho \(DP = 2PM,\,\,BQ = xQN.\) Đặt \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AD} = \overrightarrow v .\) a) Hãy biểu thị các vectơ \(\overrightarrow {AP} ,\,\,\overrightarrow {AQ} \) qua hai vectơ \(\overrightarrow u \) và \(\overrightarrow v .\) b) Tìm \(x\) để \(A,\,\,P,\,\,Q\) thẳng hàng. Lời giải chi tiết
a) Ta có: \(\overrightarrow {AP} = \overrightarrow {AD} + \overrightarrow {DP} \) \(\begin{array}{l} = \overrightarrow {AD} + \frac{2}{3}\overrightarrow {DM} \\ = \overrightarrow {AD} + \frac{2}{3}\left( {\overrightarrow {AM} - \overrightarrow {AD} } \right) = \frac{1}{3}\overrightarrow {AD} + \frac{2}{3}\overrightarrow {AM} \\ = \frac{1}{3}\overrightarrow {AD} + \frac{2}{3}.\frac{1}{2}\overrightarrow {AB} = \frac{1}{3}\overrightarrow u + \frac{1}{3}\overrightarrow v \end{array}\) Ta có: \(BQ = xQN\) \( \Rightarrow \) \(\overrightarrow {BQ} = x\overrightarrow {QN} \) \( \Leftrightarrow \) \(\overrightarrow {AQ} - \overrightarrow {AB} = x\left( {\overrightarrow {AN} - \overrightarrow {AQ} } \right)\) \(\begin{array}{l} \Leftrightarrow \,\,\left( {x + 1} \right)\overrightarrow {AQ} = \overrightarrow {AB} + x\overrightarrow {AN} \\ \Leftrightarrow \,\,\left( {x + 1} \right)\overrightarrow {AQ} = \overrightarrow {AB} + x\left( {\overrightarrow {AD} + \overrightarrow {DN} } \right) = x\overrightarrow {AD} + \overrightarrow {AB} + x.\frac{1}{2}\overrightarrow {AB} \\ \Leftrightarrow \,\,\left( {x + 1} \right)\overrightarrow {AQ} = x\overrightarrow {AD} + \left( {\frac{1}{2}x + 1} \right)\overrightarrow {AB} \\ \Leftrightarrow \,\,\left( {x + 1} \right)\overrightarrow {AQ} = x\overrightarrow v + \left( {\frac{1}{2}x + 1} \right)\overrightarrow u \\ \Leftrightarrow \,\,\overrightarrow {AQ} = \frac{{x + 2}}{{2\left( {x + 1} \right)}}\overrightarrow u + \frac{x}{{x + 1}}\overrightarrow v \end{array}\) b) Để \(A,\,\,P,\,\,Q\) thẳng hàng \( \Leftrightarrow \) \(\overrightarrow {AP} \) và \(\overrightarrow {AQ} \) cùng phương \( \Leftrightarrow \,\,\frac{{x + 2}}{{2\left( {x + 1} \right)}}:\frac{1}{3} = \frac{x}{{x + 1}}:\frac{1}{3}\) (Điều kiện: \(x \ne - 1\)) \(\begin{array}{l} \Leftrightarrow \,\,\frac{{x + 2}}{2} = x\\ \Leftrightarrow \,\,2x = x + 2\end{array}\) \( \Leftrightarrow \,\,x = 2\) (thỏa mãn) Vậy \(x = 2\) thì \(A,\,\,P,\,\,Q\) thẳng hàng
|




















Danh sách bình luận