Giải bài 4.55 trang 69 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

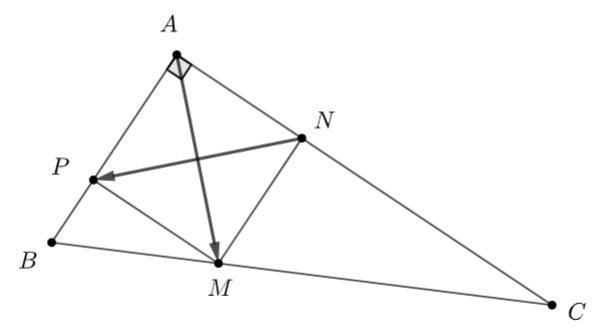
Đề bài

Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 1,\,\,AC = 2.\) Lấy \(M,\,\,N,\,\,P\) tương ứng thuộc các cạnh \(BC,\,\,CA,\,\,AB\) sao cho \(2BM = MC,\,\,CN = 2NA,\,\,AP = 2PB.\) Giá trị của tích vô hướng \(\overrightarrow {AM} .\overrightarrow {NP} \) bằng

A. \(\frac{2}{3}\)

B. \( - \frac{1}{2}\)

C. \(0\)

D. \(1\)

Lời giải chi tiết

Ta có: \(\frac{{CN}}{{CA}} = \frac{{CM}}{{CB}} = \frac{2}{3}\)

\( \Rightarrow \) \(MN\)//\(AB\) hay \(MN\)//\(AP\)       (1)

Ta có: \(\frac{{BP}}{{BA}} = \frac{{BM}}{{BC}} = \frac{1}{3}\)

\( \Rightarrow \) \(MP\)//\(AC\) hay \(MP\)//\(AN\)       (2)

Ta có: \(AP = \frac{2}{3}AB = \frac{2}{3}.1 = \frac{2}{3}\) và \(AN = \frac{1}{3}AC = \frac{2}{3}\)

Từ (1) và (2) \( \Rightarrow \) Tứ giác \(APMN\) là hình bình hành

Mặt khác \(\widehat {PAN} = {90^ \circ }\) và \(AP = AN = \frac{2}{3}\)

\( \Rightarrow \) tứ giác \(APMN\) là hình vuông

\( \Rightarrow \) \(AM \bot PN\) \( \Rightarrow \overrightarrow {AM} .\overrightarrow {NP}  = 0\)

Chọn C