Giải bài 45 trang 113 sách bài tập toán 11 - Cánh diềuPhần trong của một bể đựng nước được xây có dạng hình hộp như hình dưới đây. Để xác định tỉ số của độ cao mực nước trong bể với chiều cao của lòng bể Quảng cáo
Đề bài Phần trong của một bể đựng nước được xây có dạng hình hộp như hình dưới đây. Để xác định tỉ số của độ cao mực nước trong bể với chiều cao của lòng bể, bạn Minh làm như sau: “Lấy một thanh thước thẳng đủ dài cắm vào bể sao cho một đầu chạm đáy bể và để thước tựa vào mép dưới của thành miệng bể, đánh dấu điểm tựa. Sau đó rút thước lên, tính tỉ số độ dài của phần thước chìm trong nước và độ dài của phần thước từ điểm được đánh dấu đến điểm đầu chạm đáy bể. Tỉ số đó chính bằng tỉ số của độ cao mực nước trong bể với chiều cao lòng bể”. Bạn Minh làm có đúng không? Vì sao?
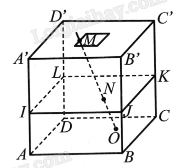
Phương pháp giải - Xem chi tiết Sử dụng định lí Thales trong không gian để chỉ ra rằng cách làm của bạn Nam là đúng hay sai. Lời giải chi tiết Giả sử phần trong bể nước và thước được biểu diễn bởi hình hộp \(ABCD.A'B'C'D'\) và đường thẳng \(MO\). Mặt nước được biểu diễn bởi mặt phẳng \(\left( {IJKL} \right)\). Khi đó, ba mặt phẳng \(\left( {ABCD} \right)\), \(\left( {IJKL} \right)\), \(\left( {A'B'C'D'} \right)\) là ba mặt phẳng song song. Nhận xét rằng hai đường thẳng \(AA'\) và \(MO\) cùng cắt 3 mặt phẳng \(\left( {ABCD} \right)\), \(\left( {IJKL} \right)\), \(\left( {A'B'C'D'} \right)\) nên theo định lí Thales trong không gian, ta có: \(\frac{{A'I}}{{MN}} = \frac{{IA}}{{NO}} = \frac{{AA'}}{{OM}} \Rightarrow \frac{{IA}}{{AA'}} = \frac{{NO}}{{OM}}\). Như vậy, bạn Minh làm như vậy là đúng.
|





















Danh sách bình luận