Giải bài 44 trang 113 sách bài tập toán 11 - Cánh diềuChứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh. Quảng cáo
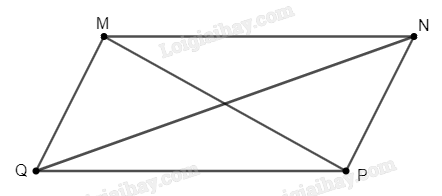
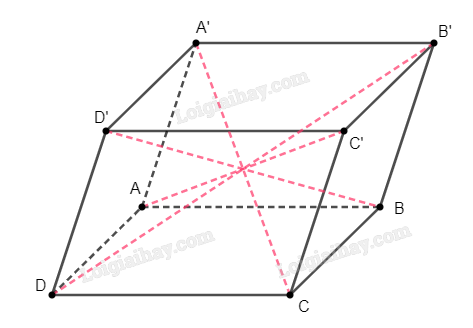
Đề bài Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh. Phương pháp giải - Xem chi tiết Trước hết, cần chứng minh kết quả phụ: Trong một hình bình hành, tổng bình phương của hai đường chéo bằng tổng bình phương tất cả các cạnh của hình bình hành. Áp dụng kết quả này vào hình hộp. Lời giải chi tiết Trước hết, ta sẽ chứng minh kết quả phụ: Trong một hình bình hành, tổng bình phương của hai đường chéo bằng tổng bình phương tất cả các cạnh của hình bình hành. Xét hình bình hành \(MNPQ\) như hình dưới đây. Ta cần chứng minh rằng \(M{P^2} + N{Q^2} = M{N^2} + N{P^2} + P{Q^2} + Q{M^2}\) Áp dụng định lí cosin trong tam giác \(MPQ\) và \(NPQ\), ta có: \(M{P^2} = Q{M^2} + Q{P^2} - 2QM.QP.\cos MQP\) \(Q{N^2} = P{Q^2} + P{N^2} - 2PN.PQ.\cos QPN\). Do \(QM = PN\) và \(\cos MQP = - \cos QPN\) (do \(\widehat {MQP}\) và \(\widehat {QPN}\) bù nhau), nên ta có \(M{P^2} + N{Q^2} = M{Q^2} + 2P{Q^2} + P{N^2} - 2QM.QP\cos MQP + 2QM.QP\cos MQP\) \( \Rightarrow M{P^2} + N{Q^2} = 2\left( {M{N^2} + N{P^2}} \right)\). Ta có điều phải chứng minh. Quay trở lại bài toán, ta xét hình hộp \(ABCD.A'B'C'D'\). Áp dụng kết quả vừa chứng minh được ở trên với hai hình bình hành \(ACC'A'\), \(DBB'D'\) và \(A'B'C'D'\) ta có: \(AC{'^2} + A'{C^2} = 2\left( {AA{'^2} + A'C{'^2}} \right)\) ; \(B'{D^2} + BD{'^2} = 2\left( {BB{'^2} + B'D{'^2}} \right)\); \(A'C{'^2} + B'D{'^2} = 2\left( {A'B{'^2} + A'D{'^2}} \right)\). Như vậy \(AC{'^2} + A'{C^2} + BD{'^2} + B'{D^2} = 2\left( {AA{'^2} + A'C{'^2} + BB{'^2} + B'D{'^2}} \right)\) \( = 4AA{'^2} + 2\left( {A'C{'^2} + B'D{'^2}} \right) = 4AA{'^2} + 4A'B{'^2} + 4A'D{'^2}\). Do \(4AA{'^2} = AA{'^2} + BB{'^2} + CC{'^2} + DD{'^2}\), \(4A'B{'^2} = A'B{'^2} + A{B^2} + C'D{'^2} + C{D^2}\), \(4A'D{'^2} = A'D{'^2} + A{D^2} + B'C{'^2} + B{C^2}\), ta kết luận rằng trong một hình hộp, tổng bình phương tất cả các đường chéo bằng tổng tất cả các cạnh của hình hộp đó. Bài toán được chứng minh.
|




















Danh sách bình luận