Giải bài 40 trang 113 sách bài tập toán 11 - Cánh diềuCho hình hộp \(ABCD.A'B'C'D'\). Quảng cáo
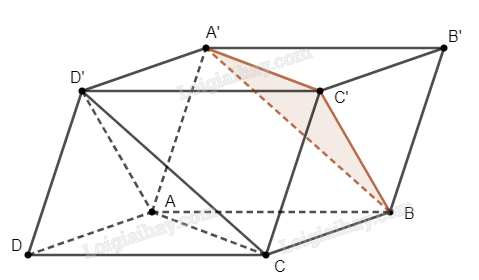
Đề bài Cho hình hộp \(ABCD.A'B'C'D'\). Mặt phẳng \(\left( {BA'C'} \right)\) song song với mặt phẳng nào dưới đây? A. \(\left( {ACD} \right)\) B. \(\left( {ADD'} \right)\) C. \(\left( {DCD'} \right)\) D. \(\left( {AD'C} \right)\) Phương pháp giải - Xem chi tiết Chỉ ra hai đường thẳng cắt nhau và song song với \(\left( {BA'C'} \right)\), mặt phẳng chứa hai đường thẳng đó là mặt phẳng cần tìm. Lời giải chi tiết
Do hình hộp là hình lăng trụ, các mặt bên là hình bình hành nên ta có \(ADD'A'\) và \(DCC'D'\) là các hình bình hành. Ta có \(A' \in \left( {ADD'A'} \right) \cap \left( {BA'C'} \right)\) nên hai mặt phẳng \(\left( {ADD'A'} \right)\) và \(\left( {BA'C'} \right)\) có điểm chung, tức là chúng không song song với nhau. Chứng minh tương tự, hai mặt phẳng \(\left( {BA'C'} \right)\) và \(\left( {DCD'} \right)\) không song song với nhau, và hai mặt phẳng \(\left( {BA'C'} \right)\) và \(\left( {ACD} \right)\) cũng không song song với nhau. Nhận xét rằng tứ giác \(ACC'A'\) có \(AA' = CC'\) và \(AA'\parallel CC'\) nên nó là hình bình hành. Suy ra \(A'C'\parallel AC\). Do \(AC \subset \left( {AD'C} \right)\) nên \(A'C'\parallel \left( {AD'C} \right)\). Chứng minh tương tự ta cũng có \(BC'\parallel \left( {AD'C} \right)\). Như vậy \(\left( {BA'C'} \right)\parallel \left( {AD'C} \right)\). Đáp án đúng D.
|




















Danh sách bình luận