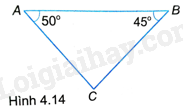
Giải bài 4.25 trang 50 sách bài tập toán 9 - Kết nối tri thức tập 1Hai trạm quan trắc tàu biển đặt ở hai mỏm núi A và B cách nhau 2km, nhìn thấy chiếc tàu C ở phía xa với (widehat {CAB} = {50^o},widehat {CBA} = {45^o}) (H.4.14). Hỏi tàu còn cách đường thẳng AB bao nhiêu mét? Quảng cáo
Đề bài Hai trạm quan trắc tàu biển đặt ở hai mỏm núi A và B cách nhau 2km, nhìn thấy chiếc tàu C ở phía xa với \(\widehat {CAB} = {50^o},\widehat {CBA} = {45^o}\) (H.4.14). Hỏi tàu còn cách đường thẳng AB bao nhiêu mét?
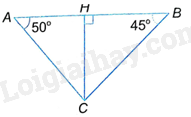
Phương pháp giải - Xem chi tiết + Kẻ đường cao AH của tam giác ABC thì H nằm giữa A và B vì hai góc A, B đều nhọn. + Tam giác ACH vuông tại H nên \(AH = HC.\cot A\) + Tam giác BCH vuông tại H nên \(BH = HC.\cot B\) + \(AB = AH + BH = HC\left( {\cot A + \cot B} \right)\) nên tính được HC. Lời giải chi tiết
Kẻ đường cao AH của tam giác ABC thì H nằm giữa A và B vì hai góc A, B đều nhọn. Tam giác ACH vuông tại H nên \(AH = HC.\cot A\) Tam giác BCH vuông tại H nên \(BH = HC.\cot B\) Do đó, \(AB = AH + BH = HC\left( {\cot A + \cot B} \right)\) Suy ra \(HC = \frac{{AB}}{{\cot A + \cot B}} \) \(= \frac{2}{{\cot {{50}^o} + \cot {{45}^o}}} \) \( \approx 1,087\left( {km} \right) = 1807m\)
|




















Danh sách bình luận