Bài 40 trang 36 Vở bài tập toán 8 tập 1Giải bài 40 trang 36 VBT toán 8 tập 1. Cho hai đa thức A = 3x^4 + x^3 + 6x - 5 và B = x^2 + 1 ... Quảng cáo
Đề bài Cho hai đa thức \(A = 3{x^4} + {x^3} + 6x - 5\) và \(B = {x^2} + 1\). Tìm dư \(R\) trong phép chia \(A\) cho \(B\) rồi viết \(A\) dưới dạng \(A = B . Q + R\). Phương pháp giải - Xem chi tiết Áp dụng quy tắc chia hai đa thức một biến đã sắp xếp. Lời giải chi tiết Thực hiện phép chia \(A\) cho \(B\) ta có: \(Q=(3{x^2} + x - 3);\) \(R=5x-2.\) Do đó \( 3{x^4} + {x^3} + 6x - 5 \)\(= ({x^2} + 1)(3{x^2} + x - 3) + 5x - 2\) Giải thích:
Loigiaihay.com
|














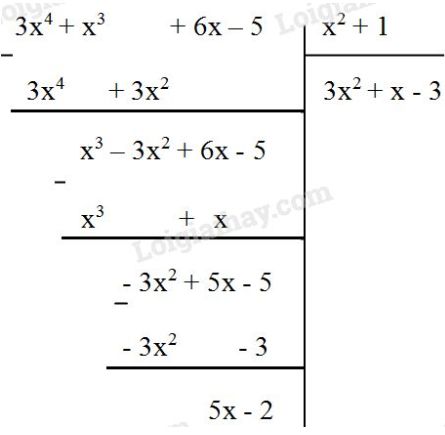






Danh sách bình luận