Bài 4 trang 7 Vở bài tập toán 8 tập 2

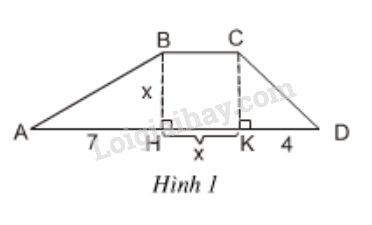
Đề bài

Tính diện tích của hình thang \(ABCD\) theo \(x\) bằng hai cách:

1) Tính theo công thức \(S = BH \times (BC + DA) : 2\);

2) \(S = {S_{ABH}} + {S_{BCKH}} + {S_{CKD}}\) 

Sau đó sử dụng giả thiết \(S = 20\) để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?

Lời giải chi tiết

1) Theo công thức \(S = BH \times (BC + DA) : 2\)

Ta có: \(DA =  7 + x + 4 = 11 + x\), \(BC=x\), \(BH=x\).

Vậy

\(S = {x\left( {x + 11 + x} \right)}:{2} \)\(\,= {x(11 + 2x)}:{2}=\dfrac{{11x + 2{x^2}}}{2}\) 

Ta có phương trình: \( \dfrac{{11x + 2{x^2}}}{2}=20\)       (1)

2) Theo công thức \(S = {S_{ABH}} + {S_{BCKH}} + {S_{CKD}}\)

Ta có: \({S_{ABH}} = \dfrac{1}{2}BH.AH = \dfrac{1}{2}x.7=\dfrac{7}{2}x\); \({S_{BCKH}} =BH.HK= x.x = {x^2}\); \({S_{CKD}} = \dfrac{1}{2}CK.KD = \dfrac{1}{2}.x.4 = 2x\)

\( S = \dfrac{7}{2}x + {x^2} + 2x  \)

Ta có phương trình \( \dfrac{7}{2}x + x^2+ 2x  = 20  \)       (2)

Trong hai phương trình trên, không có phương trình nào là phương trình bậc nhất.

Loigiaihay.com