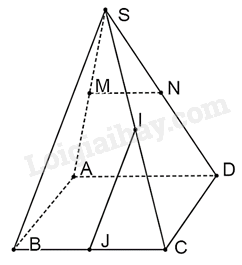
Giải bài 4 trang 51 sách bài tập toán 11 - Chân trời sáng tạo tập 2Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N, I, J lần lượt là trung điểm của SA, SD, SC và BC. Tính các góc giữa các đường thẳng sau: Quảng cáo
Đề bài Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N, I, J lần lượt là trung điểm của SA, SD, SC và BC. Tính các góc giữa các đường thẳng sau: a) IJ và DC; b) MN và IJ. Phương pháp giải - Xem chi tiết Sử dụng kiến thức về góc giữa hai đường thẳng trong không gian để tính: Góc giữa hai đường thẳng a, b trong không gian, kí hiệu (a, b), là góc giữa hai đường thẳng \(a'\) và \(b'\) cùng đi qua một điểm và lần lượt song song hoặc trùng với a và b. Góc giữa hai đường thẳng nhận giá trị từ \({0^0}\) đến \({90^0}\). Lời giải chi tiết
a) Vì I, J lần lượt là trung điểm của SC, BC nên IJ là đường trung bình của tam giác SBC. Do đó, IJ//SB. Vì tứ giác ABCD có tất cả các cạnh bằng a nên tứ giác ABCD là hình thoi. Do đó, DC//AB. Do đó, \(\left( {IJ,CD} \right) = \left( {SB,AB} \right) = \widehat {SBA}\) Tam giác SBA có ba cạnh bằng a nên tam giác SBA là tam giác đều. Suy ra, \(\widehat {SBA} = {60^0}\) b) Vì M, N lần lượt là trung điểm của SA, SD nên MN là đường trung bình của tam giác SAD. Do đó, MN//AD. Vì tứ giác ABCD là hình thoi nên AD//BC nên MN//BC. Do đó, \(\left( {MN,IJ} \right) = \left( {BC,SB} \right) = \widehat {SBC}\) Tam giác SBC có ba cạnh bằng a nên tam giác SBC đều. Suy ra \(\widehat {SBC} = {60^0}\)
|




















Danh sách bình luận