Giải bài 3 trang 48 Chuyên đề học tập Toán 12 - Chân trời sáng tạoMột công ty có ngân sách chi tiêu là (T) đồng, nếu giữ tiền mặt ({rm{x}}) đồng và đầu tư (left( {T - x} right)) đồng thì sẽ có lợi nhuận là: (fleft( x right) = frac{{aleft( {T - x} right)}}{2} - frac{{bT}}{x}), trong đó: (x): số tiền mặt cần giữ; (a): lãi suất đầu tư 30%; (b): chi phí mỗi lần rút tiền mặt 20,5%. Tìm (x) để (fleft( x right)) đạt giá trị lớn nhất khi (T = 8) tỉ đồng. Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Quảng cáo
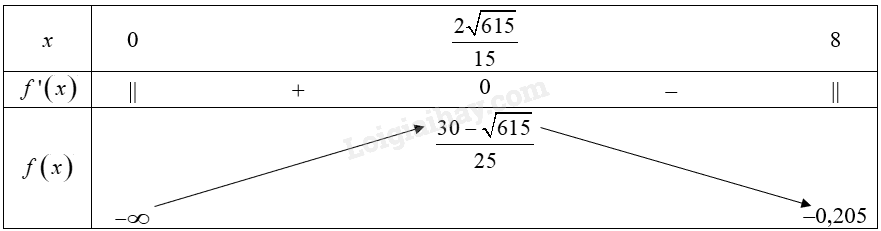
Đề bài Một công ty có ngân sách chi tiêu là \(T\) đồng, nếu giữ tiền mặt \({\rm{x}}\) đồng và đầu tư \(\left( {T - x} \right)\) đồng thì sẽ có lợi nhuận là: \(f\left( x \right) = \frac{{a\left( {T - x} \right)}}{2} - \frac{{bT}}{x}\), trong đó: \(x\): số tiền mặt cần giữ; \(a\): lãi suất đầu tư 30%; \(b\): chi phí mỗi lần rút tiền mặt 20,5%. Tìm \(x\) để \(f\left( x \right)\) đạt giá trị lớn nhất khi \(T = 8\) tỉ đồng. Phương pháp giải - Xem chi tiết Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm: ‒ Lập bảng biến thiên của hàm số trên tập hợp đó. ‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số. Lời giải chi tiết Xét hàm số \(f\left( x \right) = \frac{{30\% \left( {8 - x} \right)}}{2} - \frac{{8.20,5\% }}{x} = 0,15\left( {8 - x} \right) - \frac{{1,64}}{x} = 1,2 - 0,15x - \frac{{1,64}}{x}\) trên \(\left( {0;8} \right]\). Ta có: \(f'\left( x \right) = - 0,15 + \frac{{1,64}}{{{x^2}}}\) \(f'\left( x \right) = 0 \Leftrightarrow - 0,15 + \frac{{1,64}}{{{x^2}}} = 0 \Leftrightarrow {x^2} = \frac{{164}}{{15}} \Leftrightarrow x = \frac{{2\sqrt {615} }}{{15}}\) hoặc \(x = - \frac{{2\sqrt {615} }}{{15}}\) (loại). Bảng biến thiên của hàm số trên nửa khoảng \(\left( {0;8} \right]\):
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{\left( {0;8} \right]} f\left( x \right) = f\left( {\frac{{2\sqrt {615} }}{{15}}} \right) = \frac{{30 - \sqrt {615} }}{{25}}\). Vậy \(x = \frac{{2\sqrt {615} }}{{15}} \approx 3,3\) (tỉ đồng) để \(f\left( x \right)\) đạt giá trị lớn nhất.  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
