Bài 3 trang 112 Vở bài tập toán 8 tập 2

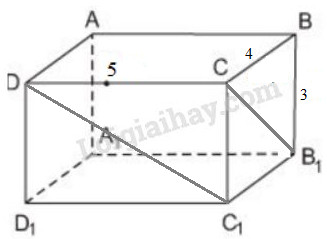
Đề bài

Các kích thước của hình hộp chữ nhật \(ABCD{A_1}{B_1}{C_1}{D_1}\) là \(DC = 5cm, CB = 4cm, BB_1= 3cm\). Hỏi độ dài \(DC_1\) và \(CB_1\) là bao nhiêu xentimét?

Lời giải chi tiết

\(B{B_1} = 3cm\) mà \(B{B_1} = C{C_1}\) nên \(C{C_1} = 3\left( {cm} \right)\).

\(DC{C_1}{D_1}\) là hình chữ nhật, do đó \(DC{C_1}\) là tam giác vuông tại \(C\).

Theo định lí Py – ta – go, ta có:

\(D{C_1} = \sqrt {D{C^2} + CC_1^2} \) \( = \sqrt {{5^2} + {3^2}}  = \sqrt {34}  \approx 5,83\left( {cm} \right)\)

\(BC{C_1}{B_1}\) cũng là hình chữ nhật nên \(BC{B_1}\) là tam giác vuông tại \(B\).

Theo định lí Py – ta – go, ta có:

\(C{B_1} = \sqrt {B{C^2} + BB_1^2} \) \( = \sqrt {{4^2} + {3^2}}  = \sqrt {25}  = 5\left( {cm} \right)\).

Loigiaihay.com