Giải bài 24 trang 69 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

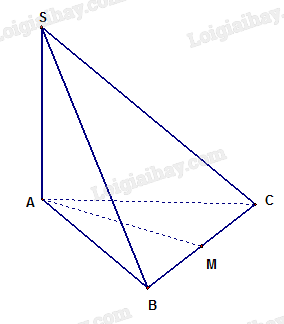
Đề bài

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(a\) và \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\). Khoảng cách giữa hai đường thẳng \(SA\) và \(BC\) bằng

A. \(\frac{{a\sqrt 2 }}{2}\).

B. \(\frac{{a\sqrt 3 }}{4}\).

C. \(\frac{{a\sqrt 6 }}{2}\).

D. \(\frac{{a\sqrt 3 }}{2}\).

Lời giải chi tiết

Gọi \(M\) là trung điểm \(BC \Rightarrow AM \bot BC\) do áy \(ABC\) là tam giác đều

Ta có \(SA \bot \left( {BC} \right) \Rightarrow AM \bot SA\)

Khoảng cách giữa hai đường thẳng \(SA\) và \(BC\) bằng \(AM = \frac{{a\sqrt 3 }}{2}\)

Chọn D