Giải bài 24 trang 104 sách bài tập toán 11 - Cánh diều

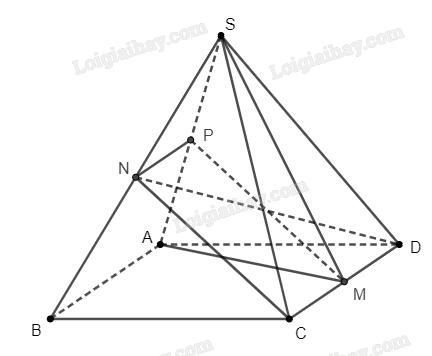
Đề bài

Cho hình chóp \(S.ABCD\) có đáy\(ABCD\) là hình bình hành. Gọi \(M\), \(N\) lần lượt là trung điểm của \(CD\), \(SB\).

a)    Xác định giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {CDN} \right)\).

b)    Chứng minh rằng đường thẳng \(CN\) song song với mặt phẳng \(\left( {SAM} \right)\).

Lời giải chi tiết

a) Vẽ \(NP\parallel AB\) với \(P \in SA\). Do \(AB\parallel CD\) nên ta suy ra \(NP\parallel CD\).

Ta có \(N \in \left( {SAB} \right) \cap \left( {CDN} \right)\), nên tồn tại giao tuyến (là đường thẳng đi qua \(N\)) của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {CDN} \right)\).

Mặt khác, ta có \(AB\parallel CD\), \(AB \subset \left( {SAB} \right)\), \(CD \subset \left( {CDN} \right)\), ta suy ra giao tuyến của \(\left( {SAB} \right)\) và \(\left( {CDN} \right)\) song song với \(CD\), tức là giao tuyến đó là đường thẳng \(NP\).

 

b) Do \(N\) là trung điểm của \(SB\), \(NP\parallel AB\) nên \(NP\) là đường trung bình của tam giác \(SAB\). Suy ra \(NP = \frac{1}{2}AB\).

Mặt khác, do \(M\) là trung điểm của \(CD\) nên \(CM = \frac{1}{2}CD\).

Như vậy \(NP = CM\). Mặt khác, ta có \(NP\parallel CM\) nên tứ giác \(CMPN\) là hình bình hành.

Từ đó \(CN\parallel MP\). Do \(MP \subset \left( {SAM} \right)\) nên \(CN\parallel \left( {SAM} \right)\).

Bài toán dược chứng minh.