Bài 2.30 trang 117 SBT giải tích 12

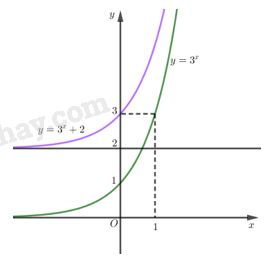
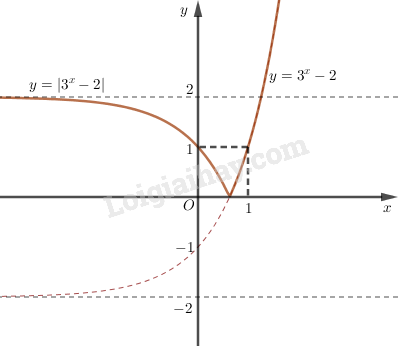
LG a

$\displaystyle y = {3^x} - 2$

Phương pháp giải:

Tịnh tiến đồ thị hàm số $y = {3^x}$ lên trên hoặc xuống dưới $2$ đơn vị.

Giải chi tiết:

Đồ thị của hàm số y $y = {3^x} - 2$  nhận được từ đồ thị của hàm số $y = {3^x}$ bằng phép tịnh tiến song song với trục tung xuống dưới $2$ đơn vị (phần đồ thị màu đỏ).

LG b

$\displaystyle y = {3^x} + 2$

Phương pháp giải:

Tịnh tiến đồ thị hàm số $y = {3^x}$ lên trên hoặc xuống dưới $2$ đơn vị.

Giải chi tiết:

Đồ thị của hàm số $y = {3^x} + 2$ nhận được từ đồ thị của hàm số $y = {3^x}$ bằng phép tịnh tiến song song với trục tung lên phía trên $2$ đơn vị (phần đồ thị màu tím).

LG c

$\displaystyle y = \left| {{3^x}-2} \right|$

Phương pháp giải:

Đồ thị hàm số $y = \left| {f\left( x \right)} \right|$ có được từ đồ thị hàm số $y = f\left( x \right)$ bằng cách:

+ Giữ nghuyên phần đồ thị hàm số $y = f\left( x \right)$ phía trên trục hoành.

+ Lấy đối xứng phần dưới qua trục hoành và xóa phần dưới cũ đi.

Giải chi tiết:

$y = \left| {{3^x} - 2} \right| = \left\{ {\begin{array}{*{20}{c}}{{3^x} - 2,khi\,\,{3^x} - 2 \ge 0}\\{ - {3^x} + 2,khi\,\,{3^x} - 2 < 0}\end{array}} \right.$

Do đó, đồ thị của hàm số $y = |{3^x} - 2|$ gồm:

- Phần đồ thị của hàm số  $y = {3^x} - 2$ ứng với ${3^x} - 2 \ge 0$ (nằm phía trên trục hoành).

- Phần đối xứng qua trục hoành của đồ thị hàm số  $y = {3^x} - 2$ ứng với ${3^x} - 2 < 0$.

Vậy đồ thị của hàm số  $y = |{3^x} - 2|$  có dạng như hình dưới.

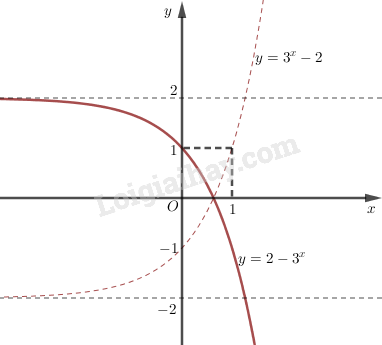
LG d

$\displaystyle y = 2-{3^x}$

Phương pháp giải:

Đồ thị hàm số $y =  - f\left( x \right)$ có được từ đồ thị hàm số $y = f\left( x \right)$ bằng cách lấy đối xứng toàn bộ đồ thị hàm số $y = f\left( x \right)$ qua trục hoành.

Giải chi tiết:

Ta có: $y = 2 - {3^x} =  - ({3^x} - 2)$

Ta có đồ thị của hàm số  $y = 2 - {3^x}$ đối xứng với đồ thị cua hàm số  $y = {3^x} - 2$ qua trục hoành.

Loigiaihay.com