Giải bài 2.19 trang 26 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

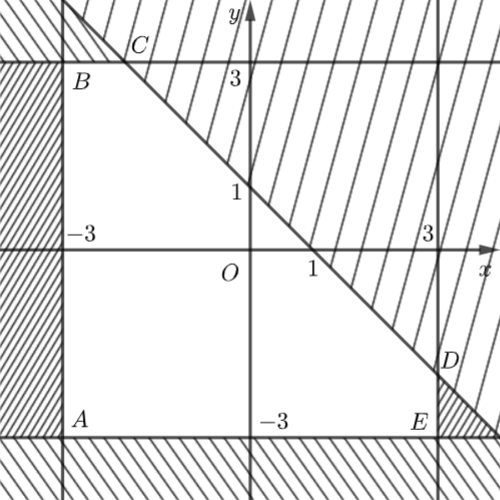
Đề bài

Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{ - 3 \le y \le 3}\\{ - 3 \le x \le 3}\end{array}} \right.\) là:

A. Miền lục giác.

B. Miền tam giác.

C. Miền tứ giác.

D. Miền ngũ giác.

Lời giải chi tiết

Miền nghiệm của bất phương trình \(x + y \le 1\) là nửa đường thẳng \(d:x + y = 1\) chứa gốc tọa độ \(O\left( {0;0} \right).\)

Miền nghiệm của bất phương trình \( - 3 \le y \le 3\) là miền nằm giữa hai đường thẳng \({d_1}:y =  - 3\) và \({d_2}:y = 3\) chứa gốc tọa độ \(O\left( {0;0} \right).\)

Miền nghiệm của bất phương trình \( - 3 \le x \le 3\) là miền nằm giữa hai đường thẳng \({d_3}:x =  - 3\) và \({d_4}:x = 3\) chứa gốc tọa độ \(O\left( {0;0} \right).\)

Miền nghiệm của hệ bất phương trình trên là ngũ giác \(ABCDE.\)

Chọn D.