Bài 2.15 trang 60 SBT hình học 12

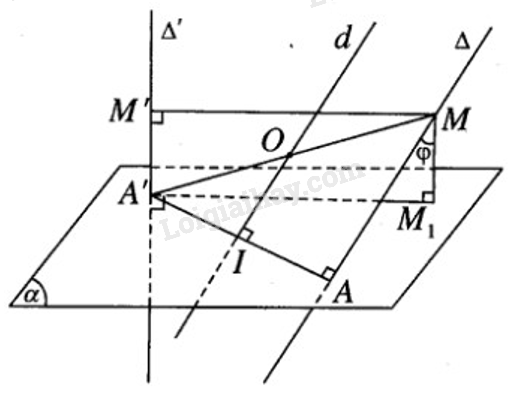
Đề bài

Cho hai đường thẳng chéo nhau $\Delta$ và $\Delta '$ có AA’ là đoạn vuông góc chung, trong đó $A \in \Delta$ và $A' \in \Delta '$. Gọi $(\alpha )$ là mặt phẳng chứa AA’ và vuông góc với  $\Delta '$ và cho biết AA’ = a. Một đường thẳng thay đổi luôn luôn song song với mặt phẳng $(\alpha )$  lần lượt cắt $\Delta$ và $\Delta '$  tại M và M’. Hình chiếu vuông góc của M trên mặt phẳng $(\alpha )$  là M₁.

a) Xác định tâm O và bán kính r của mặt cầu đi qua 5 điểm A, A’ , M , M’, M₁. Tính diện tích của mặt cầu tâm O nói trên theo a, x = A’M’ và góc $\varphi  = (\Delta ,\Delta ')$

b) Chứng minh rằng khi x thay đổi mặt cầu tâm O luôn luôn chứa một đường tròn cố định.

Lời giải chi tiết

a) Theo giả thiết ta có: $\displaystyle \widehat {A'M'M} = \widehat {A'AM} = \widehat {A'{M_1}M} = {90^0}$

Do đó 5 điểm A, A’, M, M’ ,M₁ cùng thuộc mặt cầu (S) tâm O, với O là trung điểm của A’M và có bán kính $\displaystyle r = {{A'M} \over 2}$

Mặt khác ta có A’M² = A’A² + AM², trong đó  $\displaystyle \cos \varphi  = {{M{M_1}} \over {AM}}$  nên $\displaystyle AM = {{M{M_1}} \over {\cos \varphi }} = {x \over {\cos \varphi }}$

Do đó $\displaystyle A'{M^2} = {a^2} + {{{x^2}} \over {{{\cos }^2}\varphi }}$

$\displaystyle \Rightarrow A'M = \sqrt {{{{a^2}{{\cos }^2}\varphi  + {x^2}} \over {{{\cos }^2}\varphi }}}  = {1 \over {\cos \varphi }}\sqrt {{a^2}{{\cos }^2}\varphi  + {x^2}}$

Mặt cầu tâm O có bán kính $\displaystyle r = {{A'M} \over 2} = {1 \over {2\cos \varphi }}\sqrt {{a^2}{{\cos }^2}\varphi  + {x^2}}$

Diện tích của mặt cầu tâm O là: $\displaystyle S = 4\pi {r^2} = \pi {(2r)^2} = \pi {(A'M)^2} = \pi ({a^2} + {{{x^2}} \over {{{\cos }^2}\varphi }})$

b) Gọi I là trung điểm của đoạn AA’. Ta có IO // $\displaystyle \Delta$ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với $\displaystyle \Delta$.

Mặt cầu tâm O đi qua hai điểm cố định A, A’, có tâm di động trên đường trung trực d cố định của đoạn AA’.

Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.

Loigiaihay.com