Giải bài 21 trang 67 sách bài tập toán 8 – Cánh diều

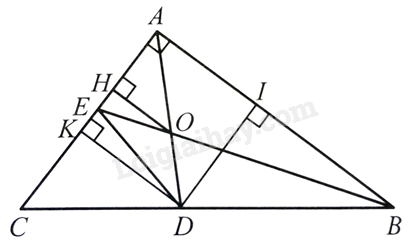
Đề bài

Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 8\) cm, \(AC = 6\) cm, có hai đường phân giác \(AD,BE\) cắt nhau tại \(O\). Tính :

a)      Độ dài các đoạn thẳng \(AE,EC\);

b)     Khoảng cách từ \(O\) đến đường thẳng \(AC\);

c)      Độ dài đường phân giác \(AD\) (theo đơn vị centimet và làm tròn kết quả đến hàng phần mười);

d)     Diện tích tam giác \(DOE\).

Lời giải chi tiết

a)      Tam giác vuông \(ABC\) vuông tại \(A\) nên theo định lí Pythagore, ta có: \(B{C^2} = A{C^2} + A{B^2} = 100\), suy ra \(BC = 10\) cm.

Vì \(BE\) là phân giác nên \(\frac{{AE}}{{EC}} = \frac{{AB}}{{BC}} = \frac{8}{{10}} = \frac{4}{5}\).

Suy ra \(\frac{{AE}}{4} = \frac{{EC}}{5} = \frac{{AE + EC}}{{4 + 5}} = \frac{6}{9} = \frac{2}{3}\). Vậy \(AE = \frac{8}{3}\) cm; \(EC = \frac{{10}}{3}\) cm.

b)     Kẻ \(OH\) vuông góc với \(AC\) tại \(H,OH \bot AC,BA \bot AC\) nên \(OH//AB\).

Suy ra \(\frac{{OH}}{{AB}} = \frac{{OE}}{{EB}}\) (1). Tam giác \(AEB\) có \(AO\) là phân giác nên \(\frac{{EO}}{{OB}} = \frac{{AE}}{{AB}} = \frac{1}{3}\).

Suy ra \(\frac{{EO}}{{EB}} = \frac{1}{4}\) (2). Từ (1) và (2) ta có \(\frac{{OH}}{{AB}} = \frac{1}{4}\), suy ra \(OH = 2\) cm.

c)      Kẻ \(DK \bot AC,DI \bot AB\). Khi đó, tứ giác \(AKDI\) có ba góc vuông và đường chéo \(AD\) là đường phân giác của góc \(KAI\) nên tứ giác \(AKDI\) là hình vuông. Suy ra \(DK = DI\). Ta có \({S_{\Delta ABC}} = {S_{\Delta ADC}} + {S_{\Delta ADB}}\) nên \(\frac{{AC.AB}}{2} = \frac{{AC.DK}}{2} + \frac{{AB.DI}}{2}\) hay \(AC.AB = AC.DK + AB.DI = \left( {AB + AC} \right)\). \(DK\) (do \(DK = DI\)). Từ đó, ta có: \(DK = \frac{{AB.AC}}{{AB + AC}} = \frac{{8.6}}{{8 + 6}} = \frac{{24}}{7}\). Tứ giác \(AKDI\) là hình vuông nên \(AD = DK\sqrt 2 \). Do đó \(AD = \frac{{24\sqrt 2 }}{7} \approx 4,8\) (cm).

d)     Ta có: \({S_{\Delta BAC}} = \frac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\). Suy ra \(\frac{{{S_{\Delta BCE}}}}{{{S_{\Delta BAC}}}} = \frac{{EC}}{{AC}} = \frac{{10}}{3}:6 = \frac{5}{9}\).

Do đó \({S_{\Delta BCE}} = \frac{5}{9}.24 = \frac{{40}}{3}\left( {c{m^2}} \right)\). Tương tự: \(\frac{{{S_{\Delta DBE}}}}{{{S_{\Delta BEC}}}} = \frac{{DB}}{{BC}} = \frac{4}{7}\).

Suy ra \({S_{\Delta DBE}} = \frac{{160}}{{21}}\left( {c{m^2}} \right)\).

Mà \(\frac{{{S_{\Delta DOE}}}}{{{S_{\Delta DBE}}}} = \frac{{OE}}{{BE}} = \frac{1}{4}\) suy ra \({S_{\Delta DOE}} = \frac{1}{4}.\frac{{160}}{{21}} = \frac{{40}}{{21}}\left( {c{m^2}} \right)\).