Bài 20 trang 144 Vở bài tập toán 9 tập 2

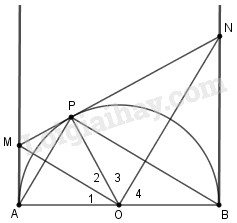
Đề bài

Cho nửa đường tròn tâm \(O\), đường kính \(AB=2R\), \(Ax\) và \(By\) là hai tiếp tuyến với nửa đường tròn tại \(A\) và \(B\). Lấy trên tia \(Ax\) điểm \(M\) rồi vẽ tiếp tuyến \(MP\) cắt \(By\) tại \(N\).

a/ Chứng minh rằng \(MON\) và \(APB\) là hai tam giác vuông đồng dạng.

b/ Chứng minh \(AM.BN = {R^2}.\)

c/ Tính tỉ số \(\dfrac{{{S_{MON}}}}{{{S_{APB}}}}\,khi\,AM = \dfrac{R}{2}.\) 

d/ Tính thể tích của hình do nửa hình tròn \(APB\) quay quanh \(AB\) sinh ra.

Lời giải chi tiết

a) \(MA//NB\) vì \(MA \bot AB\) và \(NB \bot AB.\) 

Nên \(AMNB\) là hình thang \(\widehat M + \widehat N = 180^\circ \,\left( 1 \right)\)

\(\widehat {{M_1}} = \dfrac{1}{2}\widehat M\) và \(\widehat {{N_1}} = \dfrac{1}{2}\widehat N\,\,\,\,\,(2)\) theo tính chất hai tiếp tuyến cắt nhau.

\( \Rightarrow \widehat {{N_1}} + \widehat {{M_1}} = 90^\circ ;\) Do đó, \(\widehat {MON} = 90^\circ  \Rightarrow \Delta MON\) là tam giác vuông.

\(\Delta APB\) có \(\widehat {APB} = 90^\circ \) vì góc nội tiếp chắn nửa đường tròn \(\left( {O;\dfrac{{AB}}{2}} \right)\)

Do đó, \(\Delta MON\) và \(\Delta MPO\) là hai tam giác vuông.

Theo tính chất điểm chính giữa cung ta có : \(MO \bot AP\) và \(\widehat {{O_1}} = \widehat {{O_2}}\)

\( \Rightarrow \widehat {{M_1}} = \widehat {{A_1}}\) vì là hai góc cùng phụ với hai góc bằng nhau \(\widehat {{O_1}} = \widehat {{O_2}}.\)

Vậy \(\Delta MPO \backsim \Delta MON\) vì tam giác vuông có \(\widehat {{M_1}}\) chung.

b) Xét \(\Delta MAO\) và \(\Delta NBO\) là hai tam giác vuông có \(\widehat {AMO} = \widehat {BON}\) vì cùng bằng \(90^\circ  \Rightarrow \Delta MAO \backsim \Delta OBN.\)

Do đó \(\dfrac{{AM}}{{AO}} = \dfrac{{OB}}{{BN}}\) mà \(AO = OB = R \Rightarrow AM.BN = {R^2}.\)

c) Theo tính chất của hai tiếp tuyến cắt nhau ta có : \(AM = MP;BN = NP.\)

Từ câu b)  ta có  \(AM.BN = {R^2}\) \( \Rightarrow BN = \dfrac{{{R^2}}}{{AM}}\) \( \Rightarrow MN = \dfrac{R}{2} + 2R = \dfrac{{5R}}{2}\)

Suy ra \(M{N^2} = \dfrac{{25{R^2}}}{4} \Rightarrow \dfrac{{{S_{MON}}}}{{{S_{APB}}}} = \dfrac{{M{N^2}}}{{A{B^2}}}\)\( = \dfrac{{25}}{{16}}.\)

d) Nửa hình tròn \(APB\) quay quanh \(AB\) sinh ra hình cầu bán kính \(R\)

Vậy \(V = \dfrac{4}{3}\pi {R^3}.\)

Loigiaihay.com