Bài 1.62 trang 37 SBT giải tích 12

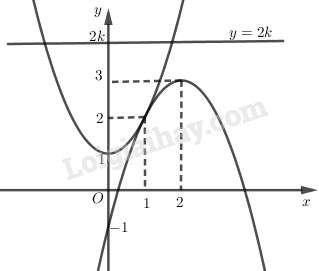
LG a

${(x - 1)^2} = 2|x - k|$

Phương pháp giải:

- Phá dấu giá trị tuyệt đối đưa về hai phương trình mới.

- Biến đổi các phương trình về dạng $f\left( x \right) = g\left( k \right)$.

- Vẽ đồ thị các hàm số $y = f\left( x \right)$ trên cùng một hệ trục tọa độ.

- Từ đó biện luận nghiệm của phương trình, sử dụng sự tương giao giữa đường thẳng $y = g\left( k \right)$ với đồ thị hàm số $y = f\left( x \right)$.

Lời giải chi tiết:

Ta có:

$\begin{array}{l} {\left( {x - 1} \right)^2} = 2\left| {x - k} \right|\\ \Leftrightarrow \left[ \begin{array}{l} 2\left( {x - k} \right) = {\left( {x - 1} \right)^2}\\ 2\left( {x - k} \right) = - {\left( {x - 1} \right)^2} \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} 2x - 2k = {x^2} - 2x + 1\\ 2x - 2k = - {x^2} + 2x - 1 \end{array} \right. \end{array}$

$\Leftrightarrow \left[ \begin{array}{l} - {x^2} + 4x - 1 = 2k\\{x^2} + 1 = 2k\end{array} \right.$

Ta vẽ đồ thị của hai hàm số: $y =  - {x^2} + 4x - 1$ và $y = {x^2} + 1$ như sau:

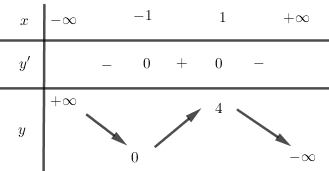
Từ đồ thị ta suy ra:

+) Nếu $2k > 3 \Leftrightarrow k > \dfrac{3}{2}$: phương trình có hai nghiệm;

+) Nếu $2k = 3 \Leftrightarrow k = \dfrac{3}{2}$: phương trình có ba nghiệm;

+) Nếu $2 < 2k < 3 \Leftrightarrow 1 < k < \dfrac{3}{2}$: phương trình có bốn nghiệm;

+) Nếu $2k = 2 \Leftrightarrow k = 1$: phương trình có ba nghiệm;

+) Nếu $1 < 2k < 2 \Leftrightarrow \dfrac{1}{2} < k < 1$: phương trình có bốn nghiệm ;

+) Nếu $2k = 1 \Leftrightarrow k = \dfrac{1}{2}$: phương trình có ba nghiệm ;

+) Nếu $2k < 1 \Leftrightarrow k < \dfrac{1}{2}$: phương trình có hai nghiệm.

Kết luận:

+) Phương trình có $4$ nghiệm $\Leftrightarrow \left[ \begin{array}{l}1 < k < \dfrac{3}{2}\\\dfrac{1}{2} < k < 1\end{array} \right.$.

+) Phương trình có $3$ nghiệm $\Leftrightarrow \left[ \begin{array}{l}k = 1\\k = \dfrac{1}{2}\\k = \dfrac{3}{2}\end{array} \right.$.

+) Phương trình có $2$ nghiệm $\Leftrightarrow \left[ \begin{array}{l}k > \dfrac{3}{2}\\k < \dfrac{1}{2}\end{array} \right.$.

LG b

${(x + 1)^2}(2 - x) = k$

Phương pháp giải:

- Khảo sát và vẽ đồ thị hàm số $y = {\left( {x + 1} \right)^2}\left( {2 - x} \right)$.

- Biện luận số nghiệm dựa vào tương giao đồ thị.

Lời giải chi tiết:

Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y = {\left( {x + 1} \right)^2}\left( {2 - x} \right)$ ta có:

$y = {\left( {x + 1} \right)^2}\left( {2 - x} \right)$ $= \left( {{x^2} + 2x + 1} \right)\left( {2 - x} \right)$ $= 2{x^2} + 4x + 2 - {x^3} - 2{x^2} - x$ $=  - {x^3} + 3x + 2$

$y' =  - 3{x^2} + 3;$$y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 1\end{array} \right.$

Bảng biến thiên:

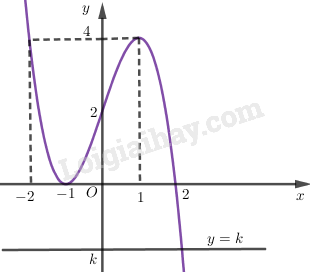
Đồ thị:

Từ đồ thị hàm số ta suy ra:

* $k > 4\;$ hoặc $k < 0$: phương trình có một nghiệm;

* $k = 4$ hoặc $k = 0$: phương trình có hai nghiệm;

* $0 < k < 4$: phương trình có ba nghiệm.

Loigiaihay.com