Giải bài 1.60 trang 35 sách bài tập toán 12 - Kết nối tri thứcCho hàm số (y = fleft( x right)) liên tục trên (mathbb{R}) và có bảng biến thiên dưới đây: Khẳng định nào dưới đây là sai? A. Giá trị nhỏ nhất của hàm số bằng -2. B. Giá trị lớn nhất của hàm số bằng 5. C. Đồ thị hàm số có hai tiệm cận ngang. D. Điểm cực tiểu của đồ thị hàm số là (left( {1;0} right)). Quảng cáo
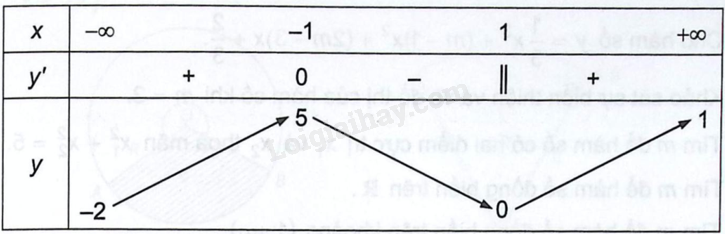
Đề bài Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như dưới đây:
Khẳng định nào dưới đây là sai? A. Giá trị nhỏ nhất của hàm số bằng -2. B. Giá trị lớn nhất của hàm số bằng 5. C. Đồ thị hàm số có hai tiệm cận ngang. D. Điểm cực tiểu của đồ thị hàm số là \(\left( {1;0} \right)\). Phương pháp giải - Xem chi tiết Quan sát bảng biến thiên và vận dụng các kiến thức về cực trị, giá trị lớn nhất, nhỏ nhất, tiệm cận đã học. Lời giải chi tiết Đáp án: A. Từ bảng biến thiên suy ra hàm số đạt giá trị lớn nhất là 5 do đó đáp án B đúng. Ngoài ra ta xác định được các tiệm cận ngang như sau, khi x tiến đến \( + \infty \) thì y tiến đến 1, x tiến đến \( - \infty \) thì y tiến đến -2 do đó đồ thị có hai tiệm cận ngang là \(y = 1\) và \(y = - 2\). Do đó C đúng. Điểm cực tiểu của đồ thị là \(\left( {1;0} \right)\) do đó D đúng. Suy ra còn lại đáp án A là sai do hàm số không có giá trị nhỏ nhất. Vậy ta chọn A.
|




















Danh sách bình luận