Bài 1.6 trang 12 SBT hình học 12

Đề bài

Tính $\sin$ của góc tạo bởi hai mặt kề nhau (tức là hai mặt có một cạnh chung) của một tứ diện đều.

Lời giải chi tiết

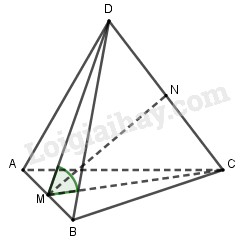
Xét tứ diện đều $ABCD$ cạnh bằng $a$. Gọi $M$ và $N$ theo thứ tự là trung điểm của $AB$ và $CD$.

Khi đó $DM \bot AB,CM \bot AB$ (trung tuyến trong tam giác đều cùng là đường cao)

Ta có: 

$\left\{ \begin{array}{l} \left( {DAB} \right) \cap \left( {CAB} \right) = AB\\ DM \bot AB\\ CM \bot AB \end{array} \right.$

$\Rightarrow$ góc giữa hai mặt phẳng $\left( {CAB} \right)$ và $\left( {DAB} \right)$ bằng góc giữa DM và CM và là góc $\widehat {CMD}$.

Xét tam giác DAM vuông tại M có $DA = a,\widehat {DAM} = {60^0}$ $\Rightarrow DM = DA\sin {60^0} = \frac{{a\sqrt 3 }}{2}$

Ta có: $\Delta DAB = \Delta CAB \Rightarrow DM = CM= \frac{{a\sqrt 3 }}{2}$

Tam giác DMC cân tại M có N là trung điểm CD nên MN vừa là đường trung tuyến vừa là đường cao.

Do đó $MN \bot CD$

Xét tam giác CMN vuông tại N có $CM = \dfrac{{a\sqrt 3 }}{2},CN = \dfrac{a}{2}$

$\Rightarrow  \sin \widehat {CMN} = \frac{{CN}}{{CM}}= \dfrac{{\dfrac{a}{2}}}{{\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{1}{{\sqrt 3 }}$

$\Rightarrow \cos \widehat {CMN}  = \sqrt {1 - {{\left( {\frac{1}{{\sqrt 3 }}} \right)}^2}} = \dfrac{{\sqrt 2 }}{{\sqrt 3 }}$

Từ đó suy ra: $\sin \widehat {CMD} = 2\sin \widehat {CMN}\cos \widehat {CMN}$$= 2.\dfrac{1}{{\sqrt 3 }}.\dfrac{{\sqrt 2 }}{{\sqrt 3 }} = \dfrac{{2\sqrt 2 }}{3}$.

Loigiaihay.com