Giải Bài 13 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

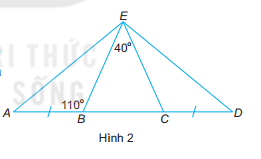
Đề bài

Cho bốn điểm A, B, C và D như Hình 2. Biết rằng \(\widehat {BEC} = {40^0};\widehat {EBA} = {110^0};AB = DC\). Chứng minh rằng:

a)Tam giác BEC cân tại đỉnh E.

b)EA = ED.

Lời giải chi tiết

a)

Ta có: \(\widehat {ABE} + \widehat {EBC} = {180^0}\)(2 góc kề bù)

\(\begin{array}{l} \Rightarrow {110^0} + \widehat {EBC} = {180^0}\\ \Rightarrow \widehat {EBC} = {180^0} - {110^0}\\ \Rightarrow \widehat {EBC} = {70^0}\end{array}\)

Xét tam giác EBC: \(\widehat E + \widehat B + \widehat C = {180^0}\) (Tổng ba góc trong tam giác)

\(\begin{array}{l} \Rightarrow {40^0} + {70^0} + \widehat C = {180^0}\\ \Rightarrow \widehat C = {180^0} - {110^0}\\ \Rightarrow \widehat C = {70^0}\\ \Rightarrow \widehat {EBC} = \widehat {ECB} = {70^0}\end{array}\)

\( \Rightarrow \Delta EBC\) cân tại E

\( \Rightarrow EB = EC\)

b)CM: EA = ED

Ta có:

\(\begin{array}{l}\widehat {ECD} = {180^0} - \widehat {ECB} = {180^0} - {70^0} = {110^0}\\ \Rightarrow \widehat {ABE} = \widehat {DCE}\end{array}\)

Xét \(\Delta ABE\)và có:

\(\begin{array}{l}BE = CE\left( {cmt} \right)\\\widehat {ABE} = \widehat {DCE}\left( {cmt} \right)\\AB = DC\left( {gt} \right)\\ \Rightarrow \Delta ABE = \Delta DCE\left( {c - g - c} \right)\\ \Rightarrow AE = DE\end{array}\)