Bài 1.15 trang 19 SBT hình học 12

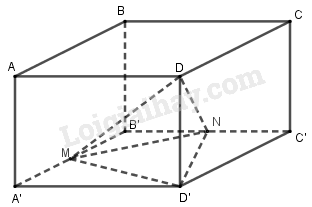
Đề bài

Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,BC = b,AA' = c\). Gọi \(M\) và \(N\) theo thứ tự là trung điểm của \(A'B'\) và \(B'C'\). Tính tỉ số giữa thể tích khối chóp \(D'.DMN\) và thể tích khối hộp chữ nhật \(ABCD.A'B'C'D'\).

Lời giải chi tiết

Thể tích khối chóp \(D'.DMN\) bằng thể tích khối chóp \(D.D'MN\)

Ta có:

\(\begin{array}{l}
{S_{A'B'C'D'}} = A'B'.B'C'={ab}\\
{S_{D'A'M}} = \frac{1}{2}A'D.A'M = \frac{1}{2}.b.\frac{a}{2} = \frac{{ab}}{4}\\
{S_{B'MN}} = \frac{1}{2}B'M.B'N = \frac{1}{2}.\frac{a}{2}.\frac{b}{2} = \frac{{ab}}{8}\\
{S_{D'C'N}} = \frac{1}{2}C'D'.C'N = \frac{1}{2}.a.\frac{b}{2} = \frac{{ab}}{4}
\end{array}\)

\({S_{D'MN}} = {S_{A'B'C'D'}} - \left( {{S_{D'A'M}} + {S_{B'MN}} + {S_{D'C'N}}} \right)\)\( = ab - \left( {\dfrac{{ab}}{4} + \dfrac{{ab}}{8} + \dfrac{{ab}}{4}} \right) = \dfrac{{3ab}}{8}\)

Thể tích khối chóp \({V_{D'.DMN}}  = \frac{1}{3}{S_{D'MN}}.DD'\) \(= \dfrac{1}{3}.\dfrac{{3ab}}{8}.c = \dfrac{{abc}}{8}\).

Lại có \({V_{ABCD.A'B'C'D'}} = abc\) \( \Rightarrow \dfrac{{{V_{D'.DMN}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{1}{8}\).

Loigiaihay.com