Bài 11 trang 95 Vở bài tập toán 9 tập 2

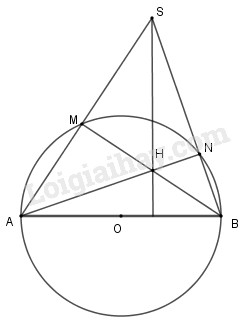
Đề bài

Cho đường tròn tâm \(O\), đường kính \(AB\) và \(S\) là một điểm nằm bên ngoài đường tròn. \(SA\) và \(SB\) lần lượt cắt đường tròn tại \(M\) và \(N\). Gọi \(H\) là giao điểm của \(BM\) và \(AN\). Chứng minh rằng \(SH\) vuông góc với \(AB\). 

Lời giải chi tiết

Vì \(M,N\) nằm trên đường tròn tâm \(O\) nên \(\widehat {AMB} = \widehat {ANB} = 90^\circ \) ( góc nội tiếp chắn nửa đường tròn)

Suy ra \(AN \bot SB\) và \(BM \bot SA.\)

Do đó, \(AN;BM\) là hai đường cao của \(\Delta SAB\) và \(H\) là giao điểm của \(AN\) và \(BM.\)

Vậy \(SH \bot AB\) vì \(H\) là trực tâm của tam giác \(ABS.\)