Giải bài 10.19 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 2Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng 1m, chiều cao bằng 2m. Người ta khoét từ hai đầu khối gỗ hai nửa hình cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa khối cầu (H.10.8). Tính tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu. Quảng cáo
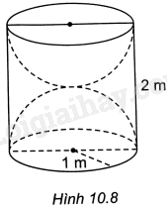
Đề bài Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng 1m, chiều cao bằng 2m. Người ta khoét từ hai đầu khối gỗ hai nửa hình cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa khối cầu (H.10.8). Tính tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu.
Phương pháp giải - Xem chi tiết + Tính thể tích V của khối gỗ hình trụ bán kính đáy bằng 1m, chiều cao bằng 2m. + Tính thể tích \({V_1}\) của hai nửa khối cầu bị khoét đi có bán kính 1m. + Tính thể tích phần còn lại của khối gỗ: \({V_2} = V - {V_1}\). + Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là: \(\frac{{{V_2}}}{V}\). Lời giải chi tiết Thể tích của khối gỗ hình trụ là: \(V = \pi {.1^2}.2 = 2\pi \left( {{m^3}} \right)\). Vì đường tròn đáy của hình trụ là đường tròn lớn của mỗi nửa hình cầu nên bán kính của mỗi nửa hình cầu là \(R = 1m\). Thể tích của hai nửa khối cầu bị khoét đi là: \({V_1} = 2.\frac{1}{2}.\frac{4}{3}\pi {.1^3} = \frac{{4\pi }}{3}\left( {{m^3}} \right)\). Thể tích phần còn lại của khối gỗ là: \({V_2} = V - {V_1} = 2\pi - \frac{{4\pi }}{3} = \frac{{2\pi }}{3}\left( {{m^3}} \right)\). Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là: \(\frac{{{V_2}}}{V} = \frac{{\frac{{2\pi }}{3}}}{{2\pi }} = \frac{1}{3}\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
