Giải Bài 10 trang 27 SGK Toán 8 tập 2 – Chân trời sáng tạo

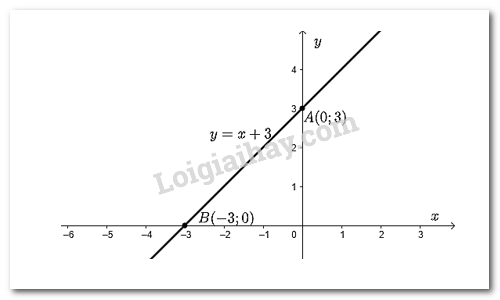
a)

a) Tính thể tích \(y\left( {{m^3}} \right)\) của nước có trong bể sau \(x\) giờ.

Phương pháp giải:

- Giả sử mỗi giờ vòi nước chảy được \(a\) \(\left( {{m^3}} \right)\) nước vào bể thì sau \(b\) giờ lượng nước từ vào đã chảy vào được trong bể là \(a.b\)\(\left( {{m^3}} \right)\).

Lượng nước có trong bể là \(a.b + c\)\(\left( {{m^3}} \right)\) với \(c\) là lượng nước có trong bể khi chưa có vòi nước chảy vào.

Lời giải chi tiết:

Vì mỗi giờ vòi nước chảy được 1 \({m^3}\) nên sau \(x\) giờ vòi đã chảy được \(1.x\) \(\left( {{m^3}} \right)\) nước.

Ban đầu trong bể chứa sẵn 3 \({m^3}\) nước nên lượng nước \(y\) có trong bể sau \(x\) giờ là:

\(y = 1.x + 3 = x + 3\).

b)

b) Vẽ đồ thị của hàm số \(y\) theo biến số \(x\).

Phương pháp giải:

- Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:

Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(A\left( {0;b} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(B\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).

Bước 2: Vẽ đường thẳng đi qua hai điểm \(A\) và \(B\). Đồ thị của hàm số \(y = ax + b\) là đường thẳng đi qua hai điểm \(A\) và \(B\).

Lời giải chi tiết:

Vẽ đồ thị hàm số \(y = x + 3\)

Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} =  - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).

Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A;B\).