Đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 6Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong cách viết sau, cách viết nào cho ta phân số?Đề bài
I. Trắc nghiệm
Câu 1 :
Trong cách viết sau, cách viết nào cho ta phân số?
Câu 2 :
Số đối của phân số \(\frac{5}{{ - 3}}\) là:
Câu 3 :
Phân số \(\frac{{ - 6}}{{15}}\) bằng:
Câu 4 :
Chọn kết quả đúng:
Câu 5 :
Mỗi đồng xu có 2 mặt (mặt S và mặt N). Tung đồng xu một lần. Mặt xuất hiện của đồng xu là?
Câu 6 :
Nếu tung đồng xu 5 lần liên tiếp, có 3 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
Câu 7 :
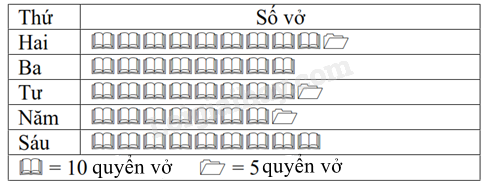
Biểu đồ tranh dưới đây cho biết số quyển vở của cửa hàng sách - thiết bị trong tuần (cửa hàng nghỉ bán thứ bảy và chủ nhật).
Ngày bán được nhiều quyển vở nhất là?
Câu 8 :
Một hộp có 7 quả bóng có 1 quả bóng xanh lá cây, 1 quả bóng đỏ, 1 quả bóng vàng, 1 quả màu tím, 1 quả màu nâu, 1 quả màu hồng, 1 quả màu xanh da trời, các quả bóng có kích thước và khối lượng như nhau. Mỗi lần bạn Hà lấy ngẫu nhiên một quả bóng ra và ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào trong hộp. Nếu Hà lấy 25 lần liên tiếp có 5 lần xuất hiện màu tím thì xác suất thực nghiệm xuất hiện màu tím bằng bao nhiêu?
Câu 10 :
Chọn câu đúng
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Trong cách viết sau, cách viết nào cho ta phân số?
Đáp án : C Phương pháp giải :
Dựa vào khái niệm về phân số. Lời giải chi tiết :
\(\frac{{0,25}}{{ - 3}}\) không phải phân số vì \(0,25 \notin \mathbb{Z}\). \(\frac{5}{0}\) không phải phân số vì 0 nằm ở mẫu. \(\frac{5}{{4,3}}\) không phải phân số vì \(4,3 \notin \mathbb{Z}\). \(\frac{{25}}{{ - 3}}\) là phân số vì \(25; - 3 \in \mathbb{Z}; - 3 \ne 0\). Đáp án C.
Câu 2 :
Số đối của phân số \(\frac{5}{{ - 3}}\) là:
Đáp án : A Phương pháp giải :
Số đối của phân số \(\frac{a}{b}\) là phân số \( - \frac{a}{b}\). Lời giải chi tiết :
Số đối của phân số \(\frac{5}{{ - 3}}\) là \(\frac{5}{3}\). Đáp án A.
Câu 3 :
Phân số \(\frac{{ - 6}}{{15}}\) bằng:
Đáp án : B Phương pháp giải :
Sử dụng quy tắc rút gọn phân số. Bước 1: Tìm ƯCLN của tử và mẫu sau khi đã bỏ dấu – (nếu có) Bước 2: Chia cả tử và mẫu cho ước chung lớn nhất vừa tìm được, ta có phân số tối giản cần tìm Lời giải chi tiết :
Ta có: \(\frac{{ - 6}}{{15}} = \frac{{ - 6:3}}{{15:3}} = \frac{{ - 2}}{5}\). Đáp án B.
Câu 4 :
Chọn kết quả đúng:
Đáp án : A Phương pháp giải :
Dựa vào quy tắc so sánh phân số Lời giải chi tiết :
So sánh \(\frac{3}{{10}}\) với \(\frac{3}{7}\): \(\frac{3}{{10}} = \frac{{3.7}}{{10.7}} = \frac{{21}}{{70}}\); \(\frac{3}{7} = \frac{{3.10}}{{7.10}} = \frac{{30}}{{70}}\). Vì \(21 < 30\) nên \(\frac{{21}}{{70}} < \frac{{30}}{{70}}\). Do đó \(\frac{3}{{10}} < \frac{3}{7}\). Nên A đúng, B sai. \(\frac{8}{{15}} < \frac{9}{{15}} = \frac{3}{5}\) nên C sai. \(\frac{{ - 8}}{{10}} < 0 < \frac{3}{{74}}\) nên D sai. Đáp án A.
Câu 5 :
Mỗi đồng xu có 2 mặt (mặt S và mặt N). Tung đồng xu một lần. Mặt xuất hiện của đồng xu là?
Đáp án : B Phương pháp giải :
Khi tung đồng xu một lần có hai kết quả có thể xảy ra với mặt xuất hiện của đồng xu, đó là: mặt S; mặt N. Lời giải chi tiết :
Mặt xuất hiện của đồng xu có thể là mặt S hoặc mặt N. Đáp án B.
Câu 6 :
Nếu tung đồng xu 5 lần liên tiếp, có 3 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
Đáp án : A Phương pháp giải :
Xác suất thực nghiệm xuất hiện mặt N khi tung đồng xu nhiều lần bằng tỉ số giữa số lần mặt N xuất hiện với tổng số lần tung đồng xu. Lời giải chi tiết :
Xác suất thực nghiệm xuất hiện mặt N là: \(\frac{3}{5}\). Đáp án A.
Câu 7 :
Biểu đồ tranh dưới đây cho biết số quyển vở của cửa hàng sách - thiết bị trong tuần (cửa hàng nghỉ bán thứ bảy và chủ nhật).
Ngày bán được nhiều quyển vở nhất là?
Đáp án : C Phương pháp giải :
Quan sát biểu đồ để xác định. Lời giải chi tiết :
Ngày thứ hai là ngày bán được nhiều quyển vở nhất (9.10 + 5 = 95 quyển) Đáp án C.
Câu 8 :
Một hộp có 7 quả bóng có 1 quả bóng xanh lá cây, 1 quả bóng đỏ, 1 quả bóng vàng, 1 quả màu tím, 1 quả màu nâu, 1 quả màu hồng, 1 quả màu xanh da trời, các quả bóng có kích thước và khối lượng như nhau. Mỗi lần bạn Hà lấy ngẫu nhiên một quả bóng ra và ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào trong hộp. Nếu Hà lấy 25 lần liên tiếp có 5 lần xuất hiện màu tím thì xác suất thực nghiệm xuất hiện màu tím bằng bao nhiêu?
Đáp án : A Phương pháp giải :
Xác suất thực nghiệm xuất hiện màu A khi lấy bóng nhiều lần bằng tỉ số giữa số lần màu A xuất hiện với tổng số lần lấy bóng. Lời giải chi tiết :
Xác suất thực nghiệm xuất hiện màu tím là: \(\frac{5}{{25}} = \frac{1}{5}\). Đáp án A.
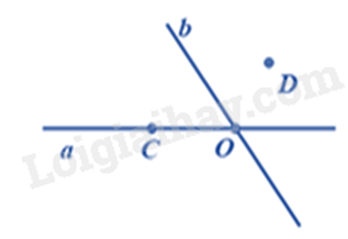
Đáp án : B Phương pháp giải :
Quan sát hình vẽ để xác định. Lời giải chi tiết :
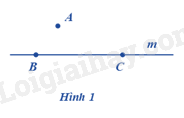
Quan sát hình vẽ ta thấy điểm A không thuộc m, điểm B, C thuộc m nên ta có: \(A \notin m;b \in m;c \in m\). Vậy đáp án đúng là B. Đáp án B.
Câu 10 :
Chọn câu đúng
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về ba điểm thẳng hàng. Lời giải chi tiết :
Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng nên C đúng. Đáp án C.
Đáp án : D Phương pháp giải :
Trung điểm của đoạn thẳng là điểm nằm giữa và cách đều hai đầu đoạn thẳng. Trung điểm của đoạn thẳng còn gọi là điểm chính giữa của đoạn thẳng. Lời giải chi tiết :
Hình 1 và hình 3 biểu diễn điểm M là trung điểm của AB. Đáp án D.
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về đoạn thẳng. Lời giải chi tiết :
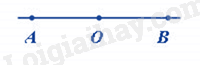
Hình vẽ có 3 đoạn thẳng, đó là: AO, OB, AB. Đáp án D.
II. Tự luận
Phương pháp giải :
1. Dựa vào quy tắc so sánh các phân số cùng tử số. 2. Sử dụng quy tắc tính với số thập phân để tìm x. Lời giải chi tiết :
1. Vì 2 < 4 < 5 < 6 nên \(\frac{1}{2} > \frac{1}{4} > \frac{1}{5} > \;\frac{1}{6}\) 2. a) \(x - \frac{3}{4} = \frac{{ - 2}}{3}\) \(\begin{array}{l}x = \frac{{ - 2}}{3} + \frac{3}{4}\\x = \frac{1}{{12}}\end{array}\) Vậy \(x = \frac{1}{{12}}\). b) \(\frac{{ - 3}}{4}:x + 1 = \frac{{ - 2}}{3}\) \(\begin{array}{l}\frac{{ - 3}}{4}:x = \frac{{ - 2}}{3} - 1\\\frac{{ - 3}}{4}:x = \frac{{ - 5}}{3}\\x = \frac{{ - 3}}{4}:\frac{{ - 5}}{3}\\x = \frac{9}{{20}}\end{array}\) Vậy \(x = \frac{9}{{20}}\). c) \(\frac{{x - 3}}{{12}} = \frac{{ - 5}}{4}\) \(\begin{array}{l}\left( {x - 3} \right).4 = - 5.12\\4\left( {x - 3} \right) = - 60\\x - 3 = - 60:4\\x - 3 = - 15\\x = - 15 + 3\\x = - 12\end{array}\) Vậy \(x = - 12\). Phương pháp giải :
Dựa vào quy tắc tính với phân số. Lời giải chi tiết :
a) \(\frac{{10}}{{11}} + \frac{3}{{11}}:3 - \frac{1}{7}\)\( = \frac{{10}}{{11}} + \frac{1}{{11}} - \frac{1}{7}\)\( = \frac{{11}}{{11}} - \frac{1}{7}\)\( = 1 - \frac{1}{7}\)\( = \frac{6}{7}\) b) \(\frac{{ - 3}}{7} + \frac{5}{{13}} + \frac{3}{7}\)\( = \left( {\frac{{ - 3}}{7} + \frac{3}{7}} \right) + \frac{5}{{13}}\)\( = 0 + \frac{5}{{13}}\)\( = \frac{5}{{13}}\) c) \(\frac{5}{3} \cdot \frac{7}{{25}} + \frac{5}{3} \cdot \frac{{21}}{{25}} - \frac{5}{3} \cdot \frac{7}{{25}}\)\( = \frac{5}{3}.\left( {\frac{7}{{25}} + \frac{{21}}{{25}} - \frac{7}{{25}}} \right)\)\( = \frac{5}{3}.\frac{{21}}{{25}}\)\( = \frac{7}{5}\) Phương pháp giải :
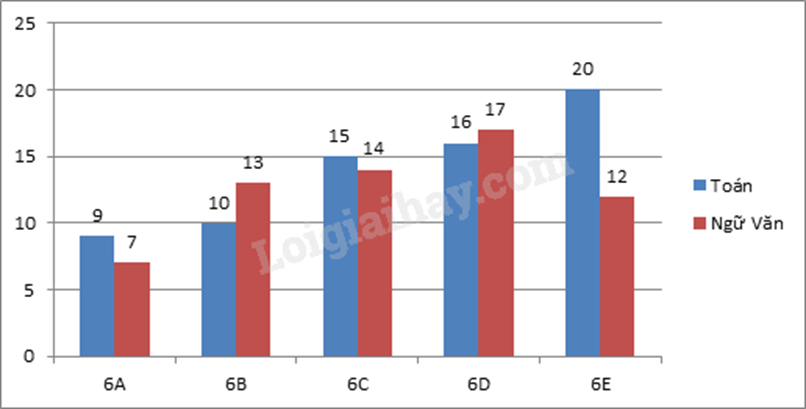
Quan sát biểu đồ để xác định. Lời giải chi tiết :
a) Số học sinh giỏi Toán của lớp 6E nhiều nhất (20 học sinh) Số học sinh giỏi Toán của lớp 6A ít nhất (9 học sinh) b) Số học sinh giỏi Ngữ văn của lớp 6D nhiều nhất (17 học sinh) Số học sinh giỏi Ngữ văn của lớp 6A ít nhất (7 học sinh) Phương pháp giải :
1. Quan sát hình vẽ để trả lời. 2. Sử dụng kiến thức về trung điểm của một đoạn thẳng. Lời giải chi tiết :
1. a) Điểm C, O thuộc đường thẳng a. b) Điểm O thuộc đường thẳng a và b. 2.
Ta có \(C\) nằm giữa \(A\) và \(B\) nên \(AC + BC = AB\) Hay \(BC = AB - AC = 7 - 3 = 4cm\). Vì \(M\) là trung điểm \(BC\) nên \(BM = \frac{{BC}}{2} = \frac{4}{2} = 2(cm)\). Vậy BM = 2cm. Phương pháp giải :
Lấy 1 – A; 1 – B. So sánh 1 – A và 1 – B từ đó ta so sánh được A và B. Lời giải chi tiết :
+) \(1 - A = 1 - \frac{{{{10}^{2022}} + 1}}{{{{10}^{2023}} + 1}} = \frac{{{{10}^{2023}} + 1}}{{{{10}^{2023}} + 1}} - \frac{{{{10}^{2022}} + 1}}{{{{10}^{2023}} + 1}} = \frac{{{{10}^{2023}} - {{10}^{2022}}}}{{{{10}^{2023}} + 1}} = \frac{{{{10}^{2022}}.9}}{{{{10}^{2023}} + 1}}\) +) \(1 - B = 1 - \frac{{{{10}^{2021}} + 1}}{{{{10}^{2022}} + 1}} = \frac{{{{10}^{2022}} + 1}}{{{{10}^{2022}} + 1}} - \frac{{{{10}^{2021}} + 1}}{{{{10}^{2022}} + 1}} = \frac{{{{10}^{2022}} - {{10}^{2021}}}}{{{{10}^{2022}} + 1}} = \frac{{{{10}^{2021}}.9}}{{{{10}^{2022}} + 1}}\) +) Để so sánh \(1 - A\) và \(1 - B\) ta so sánh \(\frac{{10}}{{{{10}^{2023}} + 1}}\) và \(\frac{1}{{{{10}^{2022}} + 1}}\) \(\frac{1}{{{{10}^{2022}} + 1}} = \frac{{10}}{{{{10}^{2023}} + 10}} < \frac{{10}}{{{{10}^{2023}} + 1}}\) Suy ra \(1 - B < 1 - A\) Suy ra \(A < B\). Vậy A < B.
|

























Danh sách bình luận