Đề số 2 – Đề kiểm tra học kì 2 – Toán 9Đáp án và lời giải chi tiết Đề số 2 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 9 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
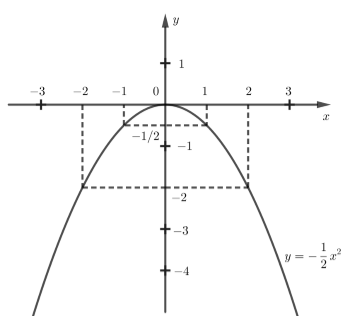
Đề bài Câu 1 (1,5 điểm): Giải các phương trình sau: a) \(3\left( {{x^2} - 5} \right) = 4x\) b) \(4{x^4} + 3{x^2} - 1 = 0\) Câu 2 (1,5 điểm): Cho hàm số: \(y = - \dfrac{1}{2}{x^2}\) có đồ thị là (P). a) Vẽ (P). b) Tìm các tọa độ giao điểm của (P) và đường thẳng (D): \(y = x - 4\) bằng phép toán. Câu 3 (1,5 điểm): Một khu vườn hình chữ nhật có chu vi 70m. Tính diện tích khu vườn biết 2 lần chiều dài nhỏ hơn 3 lần chiều rộng 5m. Câu 4 (1 điểm): Một xí nghiệp may cần thanh lý 1410 bộ quần áo. Biết mỗi ngày xí nghiệp đó bán được 30 bộ quần áo. Gọi x là số ngày đã bán, y là số bộ quần áo còn lại sau x ngày bán. a) Hãy lập công thức tính y theo x. b) Xí nghiệp cần bao nhiêu ngày để bán hết số bộ quần áo cần thanh lý? Câu 5 (1 điểm): Cho A là điểm thuộc nửa đường tròn (O) đường kính \(BC = 6cm\) và \(\angle ACB = {30^o}\). Tính AB, AC và diện tích phần tô đậm. Câu 6 (1,5 điểm): Cho phương trình: \({x^2} - 2x + m - 3 = 0\) (x là ẩn). a) Tìm m để phương trình có hai nghiệm \({x_1}\) và \({x_2}\). b) Gọi \({x_1}\) và \({x_2}\) là hai nghiệm của phương trình trên. Tìm m để \({x_1}^2 + {x_2}^2 + {x_1}^2.{x_2}^2 = 4\). Câu 7 (2 điểm): Cho \(\Delta ABC\) nhọn (\(AB < AC\)) nội tiếp đường tròn \(\left( O \right)\), các đường cao BE và CF cắt nhau tại H. a) Chứng minh tứ giác AEHF và BCEF nội tiếp. b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với \(\left( O \right)\)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh \(I{D^2} = IB.IC\). c) DE, DF cắt đường tròn \(\left( O \right)\) tại M và N. Chứng minh NM // EF. LG câu 1 Phương pháp giải: a) Sử dụng công thức nghiệm của phương trình bậc 2 để giải b) Đặt \({x^2} = t\,\,\,\left( {t \ge 0} \right)\) để đưa phương trình đề bài thành phương trình bậc 2 sau đó dùng công thức nghiệm giải tìm t sau đó tìm x. Lời giải chi tiết: a) \(3\left( {{x^2} - 5} \right) = 4x \Leftrightarrow 3{x^2} - 4x - 15 = 0\) \(\Delta ' = {2^2} + 15.3 = 49 \Rightarrow \sqrt {\Delta '} = 7\) Vậy phương trình có hai nghiệm phân biệt \({x_1} = \dfrac{{2 + 7}}{3} = 3\) và \({x_2} = \dfrac{{2 - 7}}{3} = - \dfrac{5}{3}\) b) \(4{x^4} + 3{x^2} - 1 = 0\) Đặt \({x^2} = t\,\,\,\left( {t \ge 0} \right)\) khi đó phương trình trở thành: \(4{t^2} + 3t - 1 = 0\) (1) Giải phương trình (1), ta có: \(\Delta = {3^2} + 4.4.1 = 25 \Rightarrow \sqrt \Delta = 5\) Gọi \({t_1},{t_2}\) là hai nghiệm phân biệt của (1) \( \Rightarrow \left[ \begin{array}{l}{t_1} = \dfrac{{ - 3 + 5}}{{2.4}} = \dfrac{1}{4}\,\,\,\,\,\left( {tm} \right)\\{t_2} = \dfrac{{ - 3 - 5}}{{2.4}} = - 1\,\,\,\,\left( {ktm} \right)\end{array} \right.\) Với \(t = \dfrac{1}{4}\) ta có: \({x^2} = t = \dfrac{1}{4} \Rightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\\x = - \dfrac{1}{2}\end{array} \right.\) Vậy phương trình có hai nghiệm \(x = \dfrac{1}{2}\) và \(x = - \dfrac{1}{2}.\) LG câu 2 Phương pháp giải: a) Lập bảng giá trị và vẽ đồ thị. b) Lập phương trình hoành độ giao điểm, giải phương trình bậc 2 để tìm. Lời giải chi tiết: Cho hàm số: \(y = - \dfrac{1}{2}{x^2}\) có đồ thị là (P). a) Vẽ (P). Bảng giá trị:
Vậy đồ thị hàm số \(y = - \dfrac{1}{2}{x^2}\) là đường cong đi qua các điểm \(\left( { - 2; - 2} \right),\,\,\left( { - 1; - \dfrac{1}{2}} \right),\)\(\left( {0;\,0} \right),\,\,\left( {1; - \dfrac{1}{2}} \right),\,\,\left( {2; - 2} \right).\)
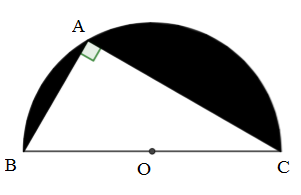
b) Tìm các tọa độ giao điểm của (P) và đường thẳng (D): \(y = x - 4\) bằng phép toán. Phương trình hoành độ giao điểm của (P) và (D) là: \( - \dfrac{1}{2}{x^2} = x - 4 \Leftrightarrow \dfrac{1}{2}{x^2} + x - 4 = 0\) Ta có: \(\Delta = 1 + 4.\dfrac{1}{2}.4 = 9 \Rightarrow \sqrt \Delta = 3 \)\(\Rightarrow x = \dfrac{{ - 1 + 3}}{1} = 2\) hoặc \(x = \dfrac{{ - 1 - 3}}{1} = - 4\) Với \(x = 2 \Rightarrow y = 2 - 4 = - 2\) Với \(x = - 4 \Rightarrow y = - 4 - 4 = - 8\) Vậy các giao điểm của (P) và (D) là 2 điểm \(A\left( {2; - 2} \right)\) và \(B\left( { - 4; - 8} \right)\) LG câu 3 Phương pháp giải: Phân tích đề bài, giải bài toán bằng cách lập hệ phương trình để tìm chiều dài chiều rộng khu vườn, sau đó tính diện tích. Diện tích hình chữ nhật bằng tích của chiều dài với chiều rộng. Lời giải chi tiết: Gọi chiều dài và chiều rộng của khu vườn lần lượt là \(x\) và \(y\,\,\,\,\left( m \right)\,\,\,\,\left( {x > \,y > 0} \right).\) Vì khu vườn hình chữ nhật có chu vi 70m nên ta có: \(2\left( {x + y} \right) = 70 \Leftrightarrow x + y = 35\,\,\,\,\left( 1 \right)\) Lại có 2 lần chiều dài nhỏ hơn 3 lần chiều rộng 5m nên ta có phương trình: \(3y - 2x = 5\,\,\,\,\,\left( 2 \right)\) Từ (1) và (2) ta có hệ phương trình: \(\begin{array}{l}\left\{ \begin{array}{l}x + y = 35\\3y - 2x = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 2y = 70\\ - 2x + 3y = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x + y = 35\\5y = 75\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 35 - y\\y = 15\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 20\,\,\,\left( {tm} \right)\\y = 15\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vì khu vườn hình chữ nhật nên diện tích khu vườn là: \(x.y = 20.15 = 300\,\,\,\left( {{m^2}} \right).\) Vậy diện tích khu vườn là \(300{m^2}.\) LG câu 4 Phương pháp giải: a) Tính số quần áo bán được sau x ngày bán từ đó suy ra y theo x. b) Bán hết thì \(y = 0\) thế vào công thức ở a) để tính số ngày x. Lời giải chi tiết: a) Mỗi ngày xí nghiệp đó bán được 30 bộ quần áo nên sau x ngày bán xí nghiệp đó bán được 30x bộ quần áo. y là số bộ quần áo còn lại sau x ngày bán \( \Rightarrow y = 1410 - 30x\) (1) b) Để xí nghiệp bán hết số bộ quần áo cần thanh lý thì \(y = 0\) Thay \(y = 0\) vào (1) ta được: \(1410 - 30x = 0\)\( \Leftrightarrow 30x = 1410 \Leftrightarrow x = 47\) (ngày) Vậy xí nghiệp cần 47 ngày để bán hết số bộ quần áo cần thanh lý. LG câu 5 Phương pháp giải: Chứng minh tam giác ABC vuông tại A từ đó sử dụng mối quan hệ giữa cạnh và góc trong tam giác vuông để tính AB, AC. Để tính diện tích phần tô đậm ta lấy diện tích nửa hình tròn (O) đường kính BC trừ đi diện tích tam giác ABC. Lời giải chi tiết:
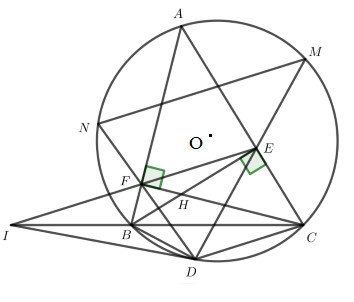
Ta có A là điểm thuộc nửa đường tròn (O) đường kính \(BC = 6cm\) \( \Rightarrow \angle BAC = {90^o}\) (góc nội tiếp chắn nửa đường tròn) Xét tam giác ABC vuông tại A ta có: \(AB = BC.\sin \angle ACB \)\(= 6.\sin {30^o} = 3\,\,(cm)\)\(AC = BC.\cos \angle ACB \)\(= 6.\cos {30^o} = 3\sqrt 3 \,\,(cm)\) Gọi diện tích nửa hình tròn (O) đường kính \(BC = 6cm\) là P \( \Rightarrow P = \dfrac{1}{2}\pi {.3^2} = \dfrac{9}{2}\pi \,\,(c{m^2})\) \( \Rightarrow P = {S_{}}\) Gọi diện tích tam giác ABC là S \( \Rightarrow S = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.3\sqrt 3 \)\(= \dfrac{{9\sqrt 3 }}{2}\,\,(c{m^2})\) Gọi diện tích phần tô đậm là Q \( \Rightarrow Q = P - S = \dfrac{9}{2}\pi - \dfrac{{9\sqrt 3 }}{2} \)\(= \dfrac{{9\pi - 9\sqrt 3 }}{2}\,\,(c{m^2})\) LG câu 6 Phương pháp giải: a) Sử dụng công thức nghiệm thu gọn, để phương trình có 2 nghiệm thì \(\Delta ' \ge 0\) b) Kết hợp câu a), biến đổi biểu thức đề bài sao cho chỉ còn \({x_1} + {x_2}\) và \({x_1}.{x_2}\), sử dụng hệ thức Vi-ét thế vào để tìm m. Lời giải chi tiết: a) Tìm m để phương trình có hai nghiệm \({x_1}\) và \({x_2}\). Xét phương trình: \({x^2} - 2x + m - 3 = 0\) Có \(\Delta ' = 1 - \left( {m - 3} \right) = - m + 4\) Phương trình có hai nghiệm \({x_1}\) và \({x_2}\) \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta ' \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\left( {lđ} \right)\\ - m + 4 \ge 0\end{array} \right. \Leftrightarrow m \le 4\) Vậy với \(m \le 4\) thì phương trình có hai nghiệm \({x_1}\) và \({x_2}\). b) Gọi \({x_1}\) và \({x_2}\) là hai nghiệm của phương trình trên. Tìm m để \({x_1}^2 + {x_2}^2 + {x_1}^2.{x_2}^2 = 4\). Theo a) để phương trình có hai nghiệm \({x_1}\) và \({x_2}\) thì \(m \le 4\) Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}.{x_2} = m - 3\end{array} \right.\) Ta có: \(\begin{array}{l}{x_1}^2 + {x_2}^2 + {x_1}^2.{x_2}^2 = 4\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}.{x_2} + {x_1}^2.{x_2}^2 = 4\\ \Leftrightarrow {2^2} - 2\left( {m - 3} \right) + {\left( {m - 3} \right)^2} = 4\\ \Leftrightarrow {\left( {m - 3} \right)^2} - 2\left( {m - 3} \right) = 0\\ \Leftrightarrow \left( {m - 3} \right)\left( {m - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 3 = 0\\m - 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\,\,\,\,\left( {tm} \right)\\m = 5\,\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy với \(m = 3\) thỏa mãn yêu cầu đề bài. LG câu 7 Phương pháp giải: a) Chứng minh A, E, H, F cùng thuộc một đường tròn để suy ra \(AEHF\) là tứ giác nội tiếp, chứng minh tứ giác BCEF có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc \(\alpha \). b) Chứng minh \(\Delta IBD \backsim \Delta IDC\) để suy ra đpcm c) Chứng minh hai góc ở vị trí đồng vị bằng nhau dựa vào các định lý Talet thuận và đảo để suy ra các tam giác đồng dạng. Lời giải chi tiết:
a) Chứng minh tứ giác AEHF và BCEF nội tiếp. Xét tứ giác \(AEHF\) có \(\angle AEH = \angle AFH = {90^o} \Rightarrow \) E, F thuộc đường tròn đường kính AH \( \Rightarrow \) A, E, H, F cùng thuộc một đường tròn đường kính \(AH\) \( \Rightarrow AEHF\) là tứ giác nội tiếp (dhnb). Xét tứ giác \(BCEF\) có \(\angle BEC = \angle BFC = {90^o}\) hay hai đỉnh \(E,F\) kề nhau cùng nhìn cạnh \(BC\) dưới các góc vuông nên BCEF là tứ giác nội tiếp (dhnb) b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với \(\left( O \right)\)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh \(I{D^2} = IB.IC\). Xét đường tròn \(\left( O \right)\) có \(\angle IDB = \angle ICD\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(BD\)) Xét \(\Delta IBD\) và \(\Delta IDC\) có: \(\angle I\) chung \(\angle IDB = \angle ICD\) (chứng minh trên) \(\begin{array}{l} \Rightarrow \Delta IBD \backsim \Delta IDC\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{ID}}{{IC}} = \dfrac{{IB}}{{ID}}\\ \Rightarrow I{D^2} = IB.IC\,\,\,\left( {đpcm} \right).\end{array}\) c) DE, DF cắt đường tròn \(\left( O \right)\) tại M và N. Chứng minh NM // EF. Vì BCEF là tứ giác nội tiếp (theo câu a) nên xét đường tròn ngoại tiếp tứ giác \(BCEF\) có \(\angle FEB = \angle FCB\) (hai góc nội tiếp cùng chắn cung \(FB\)) Xét \(\Delta IBE\) và \(\Delta IFC\) có: \(\angle I\) chung \(\angle IEB = \angle ICF\) (chứng minh trên) \(\begin{array}{l} \Rightarrow \Delta IBE \backsim \Delta IFC\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{IE}}{{IC}} = \dfrac{{IB}}{{IF}} \Rightarrow IB.IC = IE.IF\end{array}\) Theo câu b) ta có \(I{D^2} = IB.IC\) \( \Rightarrow I{D^2} = IE.IF \Rightarrow \dfrac{{ID}}{{IE}} = \dfrac{{IF}}{{ID}}\) Xét \(\Delta IDF\) và \(\Delta IED\) có: \(\angle I\) chung \(\dfrac{{ID}}{{IE}} = \dfrac{{IF}}{{ID}}\,\,\,\left( {cmt} \right)\) \( \Rightarrow \Delta IDF \backsim \Delta IED\left( {c - g - c} \right)\) \( \Rightarrow \angle IDF = \angle IED\) (2 góc tương ứng) Mặt khác, xét đường tròn \(\left( O \right)\) có ID là tiếp tuyến nên \(\angle IDF = \angle NMD\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(ND\)) \( \Rightarrow \angle IED = \angle NMD\) Mà hai góc này ở vị trí đồng vị \( \Rightarrow NM // EF.\) Nguồn sưu tầm Loigiaihay.com
|




















Danh sách bình luận