SBT Toán 12 - Kết nối tri thức

Đề minh họa kiểm tra cuối học kì 2 - SBT Toán 12 Kết nối tri thức

Làm đề thi

Phần trắc nghiệm

Đề bài

Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 35. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :

Hàm số \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên khoảng \(K\) nếu

  • A

    \(F'\left( x \right) =  - f\left( x \right),\forall x \in K\).

  • B

    \(f'\left( x \right) = F\left( x \right),\forall x \in K\).   

  • C

    \(F'\left( x \right) = f\left( x \right),\forall x \in K\).

  • D

    \(f'\left( x \right) =  - F\left( x \right),\forall x \in K\).

Câu 2 :

Nguyên hàm của hàm số \(f\left( x \right) = {x^4} + {x^2}\) là

  • A

    \(\frac{1}{5}{x^5} + \frac{1}{3}{x^3} + C\).

  • B

    \({x^4} + {x^2} + C\).

  • C

    \({x^5} + {x^3} + C\).

  • D

    \(3{x^3} + 2x + C\).

Câu 3 :

Biết \(F\left( x \right) = {x^3}\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên \(\mathbb{R}\).

Giá trị của \(\int\limits_1^3 {2f\left( x \right)dx} \) bằng

  • A

    52

  • B

    26

  • C

    54

  • D

    56

Câu 4 :

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có \(\int\limits_0^2 {f\left( x \right)dx = 9;} \int\limits_2^4 {f\left( x \right)dx = 4} .\)

Tính \(I = \int\limits_0^4 {f\left( x \right)dx} \).

  • A

    \(I = 5\).

  • B

    \(I = 36\).

  • C

    \(I = \frac{9}{4}\). 

  • D

    \(I = 13\).

Câu 5 :

Diện tích S của hình phẳng giới hạn bởi các đường \(y = 2{x^2}\), \(y =  - 1\), \(x = 0\) và \(x = 1\) được tính bởi công thức nào sau đây?

  • A

    \(S = \pi \int\limits_0^1 {\left( {2{x^2} + 1} \right)dx} \).   

  • B

    \(S = \int\limits_0^1 {\left( {2{x^2} - 1} \right)dx} \). 

  • C

    \(S = \int\limits_0^1 {{{\left( {2{x^2} + 1} \right)}^2}dx} \).

  • D

    \(S = \int\limits_0^1 {\left( {2{x^2} + 1} \right)dx} \).

Câu 6 :

Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):3x - z + 2 = 0\). Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left( P \right)\).

  • A

    \(\overrightarrow {{n_1}}  = \left( {3;0; - 1} \right)\). 

  • B

    \(\overrightarrow {{n_2}}  = \left( {3; - 1;2} \right)\).

  • C

    \(\overrightarrow {{n_3}}  = \left( {3; - 1;0} \right)\).

  • D

    \(\overrightarrow {{n_4}}  = \left( { - 1;0; - 1} \right)\).

Câu 7 :

Trong không gian Oxyz, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm  \(M\left( {1;2; - 3} \right)\) và có một vectơ pháp tuyến \(\overrightarrow n  = \left( {1; - 2;3} \right)\)?

  • A

    \(x - 2y - 3z - 6 = 0\).

  • B

    \(x - 2y + 3z - 12 = 0\).

  • C

    \(x - 2y + 3z + 12 = 0\).

  • D

    \(x - 2y - 3z + 6 = 0\).

Câu 8 :

Trong không gian Oxyz, cho đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y - 3}}{{ - 5}} = \frac{{z + 2}}{3}\). Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng d?

  • A

    \(\overrightarrow u  = \left( {1;3; - 2} \right)\).

  • B

    \(\overrightarrow u  = \left( {2; - 5;3} \right)\).

  • C

    \(\overrightarrow u  = \left( {2;5;3} \right)\).

  • D

    \(\overrightarrow u  = \left( {1;3;2} \right)\).

Câu 9 :

Trong không gian Oxyz, đường thẳng nào dưới đây đi qua điểm \(M\left( {6; - 2;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow u  = \left( {3;1; - 1} \right)\)?

  • A

    \(\frac{{x - 6}}{3} = \frac{{y + 2}}{1} = \frac{{z - 1}}{{ - 1}}\).

  • B

    \(\frac{{x + 6}}{3} = \frac{{y - 2}}{1} = \frac{{z + 1}}{{ - 1}}\).

  • C

    \(\frac{{x - 6}}{{ - 3}} = \frac{{y + 2}}{1} = \frac{{z - 1}}{{ - 1}}\). 

  • D

    \(\frac{{x - 6}}{3} = \frac{{y + 2}}{{ - 1}} = \frac{{z + 1}}{{ - 1}}\).

Câu 10 :

Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 1} \right)^2} = 2\). Xác định tọa độ tâm mặt cầu \(\left( S \right)\).

  • A

    \(I\left( { - 3;1; - 1} \right)\).

  • B

    \(I\left( {3;1; - 1} \right)\).

  • C

    \(I\left( {3; - 1;1} \right)\).

  • D

    \(I\left( { - 3; - 1;1} \right)\).

Câu 11 :

Trong không gian Oxyz, phương trình nào là phương trình mặt cầu có tâm \(I\left( {2; - 1; - 2} \right)\), bán kính bằng 3?

  • A

    \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 9\).

  • B

    \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 2} \right)^2} = 9\).

  • C

    \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 2} \right)^2} = 3\).

  • D

    \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 3\).

Câu 12 :

Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 4x + 2y + 3 = 0\). Bán kính của mặt cầu \(\left( S \right)\) là

  • A

    3

  • B

    \(\sqrt 3 \).

  • C

    \(\sqrt 2 \).

  • D

    2

Câu 13 :

Cho \(P\left( A \right) = \frac{2}{7};P\left( {B|A} \right) = \frac{1}{4};P\left( {B|\overline A } \right) = \frac{1}{5}\). Giá trị của \(P\left( B \right)\) là

  • A

    \(\frac{1}{7}\).

  • B

    \(\frac{3}{{14}}\).

  • C

    \(\frac{1}{{14}}\).

  • D

    \(\frac{2}{7}\).

Câu 14 :

Cho hai biến cố A, B sao cho \(P\left( A \right) = 0,4;P\left( {A|B} \right) = 0,7;P\left( {B|A} \right) = 0,3\). Tính \(P\left( {\overline B } \right)\)

  • A

    0,21.

  • B

    0,28.

  • C

    \(\frac{6}{{35}}\).

  • D

    \(\frac{{29}}{{35}}\).

Câu 15 :

Họ nguyên hàm của hàm số \(f\left( x \right) = 3{x^2} + \sin x\) là

  • A

    \({x^3} + \cos x + C\).

  • B

    \(6x + \cos x + C\).

  • C

    \({x^3} - \cos x + C\).

  • D

    \(6x - \cos x + C\).

Câu 16 :

Cho \(\int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx}  = 5\). Tính \(I = \int\limits_0^{\frac{\pi }{2}} {\left[ {f\left( x \right) + 2\sin x} \right]dx} \).

  • A

    7.

  • B

    \(5 + \frac{\pi }{2}\).

  • C

    \(5 + \pi \).

  • D

    3.

Câu 17 :

Biết \(\int\limits_1^3 {\frac{{x + 2}}{x}dx}  = a + b\ln c\), với \(a,b,c \in \mathbb{R},c > 0\). Tính tổng \(S = a + b + c\).

  • A

    5.

  • B

    6.

  • C

    7.

  • D

    8.

Câu 18 :

Cho hình phẳng D giới hạn bởi đồ thị hàm số  \(y = \sqrt {{x^2} + 1} \), trục hoành và hai đường thẳng \(x = 0,x = 1\). Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích là

  • A

    \(\frac{4}{3}\).

  • B

    \(\frac{{4\pi }}{3}\).

  • C

    \(2\pi \).

  • D

    2.

Câu 19 :

Cho hai mặt phẳng \(\left( \alpha  \right):3x - 2y + 2z + 7 = 0\), \(\left( \beta  \right):5x - 4y + 3z + 1 = 0\). Phương trình mặt phẳng đi qua gốc tọa độ O đồng thời vuông góc với cả hai mặt phẳng \(\left( \alpha  \right)\) và \(\left( \beta  \right)\) là

  • A

    \(2x - y - 2z = 0\).

  • B

    \(2x - y + 2z = 0\).

  • C

    \(2x + y - 2z = 0\).

  • D

    \(2x + y - 2z + 1 = 0\).

Câu 20 :

Trong không gian Oxyz cho 3 điểm \(A\left( {1; - 2;3} \right),B\left( {2;0;1} \right),C\left( {3; - 2;0} \right)\). Phương trình mặt phẳng đi qua 3 điểm \(A,{\rm{ }}B,{\rm{ }}C\) là

  • A

    \(6x + y - 4z = 16\).

  • B

    \(6x - y - 4z = 16\).

  • C

    \(6x + y + 4z = 16\).

  • D

    \(6x - y + 4z = 16\).

Câu 21 :

Trong không gian Oxyz cho điểm \(A\left( {1;2; - 1} \right)\) và mặt phẳng \(\left( P \right):x + 3y - 2z - 1 = 0\). Phương trình đường thẳng đi qua điểm \(A\) và vuông góc với mặt phẳng \(\left( P \right)\) là

  • A

    \(\frac{{x + 1}}{1} = \frac{{y + 2}}{3} = \frac{{z - 1}}{{ - 2}}\).

  • B

    \(\frac{{x - 1}}{1} = \frac{{y - 2}}{3} = \frac{{z + 1}}{{ - 2}}\).

  • C

    \(\frac{{x + 1}}{{ - 1}} = \frac{{y + 2}}{{ - 3}} = \frac{{z - 1}}{{ - 2}}\).

  • D

    \(\frac{{x - 1}}{1} = \frac{{y - 2}}{3} = \frac{{z + 1}}{2}\).

Câu 22 :

Trong không gian Oxyz cho hai điểm \(M\left( {1;0;1} \right)\) và \(N\left( {3;2; - 1} \right)\). Đường thẳng \(MN\) có phương trình tham số là

  • A

    \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2t\\z = 1 + t.\end{array} \right.\)

  • B

    \(\left\{ \begin{array}{l}x = 1 + t\\y = t\\z = 1 + t.\end{array} \right.\)

  • C

    \(\left\{ \begin{array}{l}x = 1 + t\\y = t\\z = 1 - t.\end{array} \right.\)

  • D

    \(\left\{ \begin{array}{l}x = 1 - t\\y = t\\z = 1 + t.\end{array} \right.\)

Câu 23 :

Trong không gian Oxyz cho hai điểm \(A\left( {2;4;1} \right)\) và \(B\left( { - 2;2; - 3} \right)\). Phương trình mặt cầu đường kính \(AB\) là

  • A

    \({x^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 9\).

  • B

    \({x^2} + {\left( {y - 3} \right)^2} + {\left( {z - 1} \right)^2} = 36\).

  • C

    \({x^2} + {\left( {y + 3} \right)^2} + {\left( {z - 1} \right)^2} = 9\).

  • D

    \({x^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 36\).

Câu 24 :

Sử dụng dữ kiện sau để trả lời:

Bạn An có một túi gồm 8 viên bi đen và 6 viên bi trắng. An lấy ngẫu nhiên một viên bi trong túi để cho Việt, rồi lại lấy ngẫu nhiên tiếp một viên bi nữa trong túi và cũng đưa cho Việt.

Xác suất để Việt nhận được 2 viên bi trắng là

  • A

    \(\frac{3}{7}\).

  • B

    \(\frac{{15}}{{91}}\).                   

  • C

    \(\frac{{30}}{{91}}\).

  • D

    \(\frac{{15}}{{182}}\).

Câu 25 :

Sử dụng dữ kiện sau để trả lời:

Bạn An có một túi gồm 8 viên bi đen và 6 viên bi trắng. An lấy ngẫu nhiên một viên bi trong túi để cho Việt, rồi lại lấy ngẫu nhiên tiếp một viên bi nữa trong túi và cũng đưa cho Việt.

Xác suất để Việt nhận được viên bi đen ở lần thứ nhất và viên bi trắng ở lần thứ hai là

  • A

    \(\frac{3}{7}\).

  • B

    \(\frac{{15}}{{91}}\).

  • C

    \(\frac{{30}}{{91}}\).

  • D

    \(\frac{{15}}{{182}}\).

Câu 26 :

Một xạ thủ bắn vào bia số 1 và bia số 2. Xác suất để xạ thủ đó bắn trúng bia số 1 là 0,8 và bắn trúng bia số 2 là 0,9. Xác suất để xạ thủ đó bắn trúng cả hai bia là 0,75. Biết xạ thủ đó bắn không trúng bia số 1, xác suất để xạ thủ đó bắn trúng bia số 2 là

  • A

    \(\frac{{41}}{{50}}\).

  • B

    \(\frac{9}{{50}}\).

  • C

    \(\frac{1}{4}\).

  • D

    \(\frac{3}{4}\).

Câu 27 :

Họ nguyên hàm của hàm số \(y = {e^x}\left( {2 + \frac{{{e^{ - x}}}}{{{{\cos }^2}x}}} \right)\) là

  • A

    \(2{e^x} - \frac{1}{{\cos x}} + C\).

  • B

    \(2{e^x} - \tan x + C\).

  • C

    \(2{e^x} + \tan x + C\).

  • D

    \(2{e^x} + \frac{1}{{\cos x}} + C\).

Câu 28 :

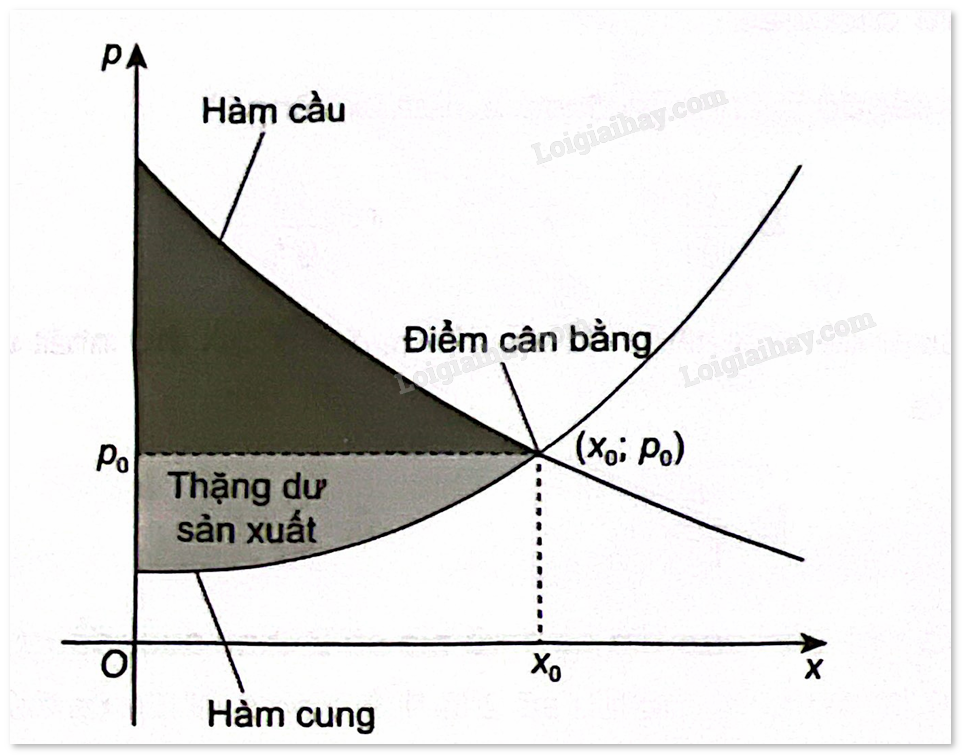
Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau \(\left( {{x_0};{p_0}} \right)\) của đồ thị hàm cầu \(y = D\left( x \right)\) và đồ thị hàm cung \(p = S\left( x \right)\) được gọi là điểm cân bằng. Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang \(p = {p_0}\) và đường thẳng đứng \(x = 0\) là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị hàm cung, đường nằm ngang \(p = {p_0}\) và đường thẳng đứng \(x = 0\) được gọi là thặng dư sản xuất, như hình vẽ sau:

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: \(y =  - 0,01{e^x} + 19\) và hàm cung \(p = 0,09{e^x} + 1\) trong đó \(x\) là số đơn vị sản phẩm. Thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này lần lượt là (làm tròn kết quả đến chữ số thập phân thứ hai)?

  • A

    68,01 và 7,57.

  • B

    68,02 và 7,56.

  • C

    69,02 và 7,56.

  • D

    70,02 và 7,66.

Câu 29 :

Một ô tô đang chạy với vận tốc 10 m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) =  - 5t + 10\) (m/s), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

  • A

    0,2 m.

  • B

    2 m.  

  • C

    10 m.

  • D

    20 m.

Câu 30 :

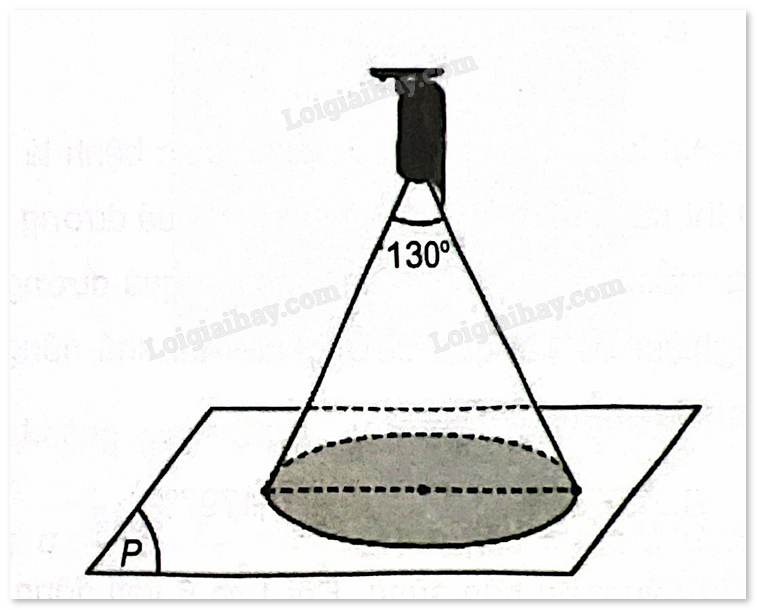
Góc quan sát ngang của một camera là \({130^ \circ }\). Trong không gian \(Oxyz\), camera được đặt tại điểm \(C\left( {1;2;2} \right)\) và chiếu thẳng về phía mặt phẳng \(\left( P \right):x + 2y - 2z + 5 = 0\). Hỏi vùng quan sát được trên mặt phẳng \(\left( P \right)\) của camera là hình tròn có diện tích bằng bao nhiêu? (làm tròn kết quả đến chữ số thập phân thứ nhất).

  • A

    57,7.

  • B

    57,8.

  • C

    56,7. 

  • D

    56,8.

Câu 31 :

Trong không gian \(Oxyz\), cho các đường thẳng:

\(\left( {{d_1}} \right):\frac{{x - 3}}{1} = \frac{{y + 1}}{{ - 2}} = \frac{{z + 1}}{1}\),                               \(\left( {{d_2}} \right):\frac{x}{1} = \frac{y}{{ - 2}} = \frac{{z - 1}}{1}\),

\(\left( {{d_3}} \right):\frac{{x - 1}}{1} = \frac{{y + 1}}{1} = \frac{{z - 1}}{1}\),                                \(\left( {{d_4}} \right):\frac{x}{1} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 1}}{1}\).

Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là

  • A

    1.

  • B

    2.

  • C

    0.

  • D

    Vô số.

Câu 32 :

Biết rằng nếu vị trí \(M\) có vĩ độ và kinh độ tương ứng là \({\alpha ^ \circ }N,{\beta ^ \circ }E\left( {0 < \alpha ,\beta  < 90} \right)\) thì có tọa độ \(M\left( {\cos {\alpha ^ \circ }\cos {\beta ^ \circ };\cos {\alpha ^ \circ }\sin {\beta ^ \circ };\sin {\alpha ^ \circ }} \right)\). Biết một đơn vị dài trong không gian \(Oxyz\) tương ứng với 6371 km trong thực tế. Khoảng cách trên mặt đất từ vị trí \(P:{30^ \circ }N{45^ \circ }E\) đến vị trí \(Q:{60^ \circ }N{45^ \circ }E\) là (tính chính xác tới chữ số thập phân thứ 4 sau dấu phẩy theo đơn vị kilômét)?

  • A

    3335,8475 km.

  • B

    3335,8478 km.

  • C

    3355,8478 km.

  • D

    3355,8475 km.

Câu 33 :

Có hai chuồng thỏ. Chuồng I có 6 con thỏ đen và 10 con thỏ trắng. Chuồng II có 8 con thỏ đen và 4 con thỏ trắng. Trước tiên, từ chuồng I lấy ra ngẫu nhiên một con thỏ rồi cho vào chuồng II. Sau đó, từ chuồng II lấy ra ngẫu nhiên một con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng.

  • A

    \(\frac{5}{{13}}\).

  • B

    \(\frac{{37}}{{104}}\).

  • C

    \(\frac{4}{{13}}\).

  • D

    \(\frac{{35}}{{104}}\).

Câu 34 :

Giả sử có một loại bệnh mà tỉ lệ người mắc bệnh là 0,01%. Nếu một người mắc bệnh thì xác suất xét nghiệm cho kết quả dương tính là 90%, nếu một người không mắc bệnh thì xác suất cho kết quả dương tính là 5%. Khi một người xét nghiệm có kết quả dương tính thì khả năng mắc bệnh của người đó là bao nhiêu phần trăm?

  • A

    0,01%.  

  • B

    4,9995%.

  • C

    0,1797%.

  • D

    0,001%.

Câu 35 :

Có hai đội thi đấu môn bắn súng. Đội I có 6 vận động viên, đội II có 8 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên trong hai đội. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I.

  • A

    \(\frac{{39}}{{140}}\).  

  • B

    \(\frac{{39}}{{83}}\).

  • C

    \(\frac{{43}}{{83}}\).

  • D

    \(\frac{{37}}{{140}}\).

Phần II: Tự luận.
Thí sinh trả lời từ câu 36 đến câu 38.
Câu 1 :

Hình bên dưới là một cánh cửa gỗ, phần dưới có dạng hình chữ nhật \(ABCD\) và mép trên là một phần của đường parabol với kích thước như sau: \(AB = 2,2m,{\rm{ }}AD = 4m,{\rm{ }}EO = 5,5m\). Biết giá thành sản xuất cửa là \(30\) triệu đồng\(/{m^2}\). Tính tổng chi phí để sản xuất cửa gỗ đã cho (làm tròn tới chữ số hàng phần trăm của triệu đồng).
Câu 2 :

Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x + 2y - 2z + 3 = 0\) và đường thẳng

\(d:\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{z}{1}\). Tính góc tạo bởi đường thẳng \(d\) và mặt phẳng \(\left( P \right)\).
Câu 3 :

Trong một hộp kín có 10 chiếc bút bi xanh và 6 chiếc bút bi đỏ đều có kích thước và khối lượng như nhau. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi từ trong hộp, không trả lại. Sau đó bạn Tùng lấy ngẫu nhiên một trong 15 chiếc bút còn lại. Tính xác suất bạn Sơn lấy được chiếc bút bi xanh và Tùng lấy được chiếc bút bi đỏ.

Lời giải và đáp án

Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 35. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :

Hàm số \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên khoảng \(K\) nếu

  • A

    \(F'\left( x \right) =  - f\left( x \right),\forall x \in K\).

  • B

    \(f'\left( x \right) = F\left( x \right),\forall x \in K\).   

  • C

    \(F'\left( x \right) = f\left( x \right),\forall x \in K\).

  • D

    \(f'\left( x \right) =  - F\left( x \right),\forall x \in K\).

Đáp án : C

Phương pháp giải :

Hiểu rõ khái niệm nguyên hàm của một hàm số trên một khoảng.

Lời giải chi tiết :

\(F'\left( x \right) = f\left( x \right),\forall x \in K\).

Câu 2 :

Nguyên hàm của hàm số \(f\left( x \right) = {x^4} + {x^2}\) là

  • A

    \(\frac{1}{5}{x^5} + \frac{1}{3}{x^3} + C\).

  • B

    \({x^4} + {x^2} + C\).

  • C

    \({x^5} + {x^3} + C\).

  • D

    \(3{x^3} + 2x + C\).

Đáp án : A

Phương pháp giải :

Áp dụng công thức nguyên hàm của hàm lũy thừa.

Lời giải chi tiết :

Ta có \(\int {f\left( x \right)dx}  = \int {\left( {{x^4} + {x^2}} \right)dx}  = \int {{x^4}dx}  + \int {{x^2}dx}  = \frac{{{x^5}}}{5} + \frac{{{x^3}}}{3} + C\).

Câu 3 :

Biết \(F\left( x \right) = {x^3}\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên \(\mathbb{R}\).

Giá trị của \(\int\limits_1^3 {2f\left( x \right)dx} \) bằng

  • A

    52

  • B

    26

  • C

    54

  • D

    56

Đáp án : A

Phương pháp giải :

Tính hàm \(f\left( x \right)\) sau đó thay vào \(\int\limits_1^3 {2f\left( x \right)dx} \).

Lời giải chi tiết :

Ta có \(f\left( x \right) = F'\left( x \right) = 3{x^2}\) suy ra \(\int\limits_1^3 {2f\left( x \right)dx}  = \int\limits_1^3 {2 \cdot 3{x^2}dx}  = \left. {6 \cdot \frac{{{x^3}}}{3}} \right|_1^3 = 52\).

Câu 4 :

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có \(\int\limits_0^2 {f\left( x \right)dx = 9;} \int\limits_2^4 {f\left( x \right)dx = 4} .\)

Tính \(I = \int\limits_0^4 {f\left( x \right)dx} \).

  • A

    \(I = 5\).

  • B

    \(I = 36\).

  • C

    \(I = \frac{9}{4}\). 

  • D

    \(I = 13\).

Đáp án : D

Phương pháp giải :

Áp dụng tính chất phép cộng tích phân.

Lời giải chi tiết :

Ta có \(I = \int\limits_0^4 {f\left( x \right)dx}  = \int\limits_0^2 {f\left( x \right)dx}  + \int\limits_2^4 {f\left( x \right)dx}  = 9 + 4 = 13.\)

Câu 5 :

Diện tích S của hình phẳng giới hạn bởi các đường \(y = 2{x^2}\), \(y =  - 1\), \(x = 0\) và \(x = 1\) được tính bởi công thức nào sau đây?

  • A

    \(S = \pi \int\limits_0^1 {\left( {2{x^2} + 1} \right)dx} \).   

  • B

    \(S = \int\limits_0^1 {\left( {2{x^2} - 1} \right)dx} \). 

  • C

    \(S = \int\limits_0^1 {{{\left( {2{x^2} + 1} \right)}^2}dx} \).

  • D

    \(S = \int\limits_0^1 {\left( {2{x^2} + 1} \right)dx} \).

Đáp án : D

Phương pháp giải :

Áp dụng công thức tính diện tích hình phẳng ứng dụng tích phân.

Lời giải chi tiết :

Trên khoảng \(\left( {0;1} \right)\) đồ thị hàm số \(y = 2{x^2}\) nằm trên \(y =  - 1\).

Câu 6 :

Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):3x - z + 2 = 0\). Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left( P \right)\).

  • A

    \(\overrightarrow {{n_1}}  = \left( {3;0; - 1} \right)\). 

  • B

    \(\overrightarrow {{n_2}}  = \left( {3; - 1;2} \right)\).

  • C

    \(\overrightarrow {{n_3}}  = \left( {3; - 1;0} \right)\).

  • D

    \(\overrightarrow {{n_4}}  = \left( { - 1;0; - 1} \right)\).

Đáp án : A

Phương pháp giải :

Từ phương trình mặt phẳng suy ra vectơ pháp tuyến.

Lời giải chi tiết :

\(\overrightarrow {{n_1}}  = \left( {3;0; - 1} \right)\) là vecto pháp tuyến của mặt phẳng.

Câu 7 :

Trong không gian Oxyz, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm  \(M\left( {1;2; - 3} \right)\) và có một vectơ pháp tuyến \(\overrightarrow n  = \left( {1; - 2;3} \right)\)?

  • A

    \(x - 2y - 3z - 6 = 0\).

  • B

    \(x - 2y + 3z - 12 = 0\).

  • C

    \(x - 2y + 3z + 12 = 0\).

  • D

    \(x - 2y - 3z + 6 = 0\).

Đáp án : C

Phương pháp giải :

Sử dụng công thức của phương trình mặt phẳng.

Lời giải chi tiết :

Do mặt phẳng có vectơ pháp tuyến là \(\overrightarrow n  = \left( {1; - 2;3} \right)\) nên ta chọn đáp án B hoặc C.

Kiểm tra xem mặt phẳng có chứa \(M\left( {1;2; - 3} \right)\) hay không.

Xét B: Thay \(M\left( {1;2; - 3} \right)\) vào \(x - 2y + 3z - 12 = 0\) ta được \(1 - 4 - 9 - 12 = 0 \Leftrightarrow  - 24 = 0\) (vô lý).

Câu 8 :

Trong không gian Oxyz, cho đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y - 3}}{{ - 5}} = \frac{{z + 2}}{3}\). Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng d?

  • A

    \(\overrightarrow u  = \left( {1;3; - 2} \right)\).

  • B

    \(\overrightarrow u  = \left( {2; - 5;3} \right)\).

  • C

    \(\overrightarrow u  = \left( {2;5;3} \right)\).

  • D

    \(\overrightarrow u  = \left( {1;3;2} \right)\).

Đáp án : B

Phương pháp giải :

Sử dụng công thức của phương trình theo đoạn chắn.

Lời giải chi tiết :

\(\overrightarrow u  = \left( {2; - 5;3} \right)\) là vecto chỉ phương của đường thẳng.

Câu 9 :

Trong không gian Oxyz, đường thẳng nào dưới đây đi qua điểm \(M\left( {6; - 2;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow u  = \left( {3;1; - 1} \right)\)?

  • A

    \(\frac{{x - 6}}{3} = \frac{{y + 2}}{1} = \frac{{z - 1}}{{ - 1}}\).

  • B

    \(\frac{{x + 6}}{3} = \frac{{y - 2}}{1} = \frac{{z + 1}}{{ - 1}}\).

  • C

    \(\frac{{x - 6}}{{ - 3}} = \frac{{y + 2}}{1} = \frac{{z - 1}}{{ - 1}}\). 

  • D

    \(\frac{{x - 6}}{3} = \frac{{y + 2}}{{ - 1}} = \frac{{z + 1}}{{ - 1}}\).

Đáp án : A

Phương pháp giải :

Áp dụng công thức phương trình đường thẳng theo đoạn chắn.

Lời giải chi tiết :

Đường thẳng đi qua điểm \(M\left( {6; - 2;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow u  = \left( {3;1; - 1} \right)\) là \(\frac{{x - 6}}{3} = \frac{{y + 2}}{1} = \frac{{z - 1}}{{ - 1}}\).

Câu 10 :

Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 1} \right)^2} = 2\). Xác định tọa độ tâm mặt cầu \(\left( S \right)\).

  • A

    \(I\left( { - 3;1; - 1} \right)\).

  • B

    \(I\left( {3;1; - 1} \right)\).

  • C

    \(I\left( {3; - 1;1} \right)\).

  • D

    \(I\left( { - 3; - 1;1} \right)\).

Đáp án : D

Phương pháp giải :

Áp dụng công thức phương trình mặt cầu.

Lời giải chi tiết :

Tâm mặt cầu là \(I\left( { - 3; - 1;1} \right)\).

Câu 11 :

Trong không gian Oxyz, phương trình nào là phương trình mặt cầu có tâm \(I\left( {2; - 1; - 2} \right)\), bán kính bằng 3?

  • A

    \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 9\).

  • B

    \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 2} \right)^2} = 9\).

  • C

    \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 2} \right)^2} = 3\).

  • D

    \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 3\).

Đáp án : B

Phương pháp giải :

Áp dụng công thức phương trình mặt cầu.

Lời giải chi tiết :

Phương trình mặt cầu có tâm \(I\left( {2; - 1; - 2} \right)\), bán kính bằng 3 là \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 2} \right)^2} = 9\).

Câu 12 :

Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 4x + 2y + 3 = 0\). Bán kính của mặt cầu \(\left( S \right)\) là

  • A

    3

  • B

    \(\sqrt 3 \).

  • C

    \(\sqrt 2 \).

  • D

    2

Đáp án : C

Phương pháp giải :

Áp dụng công thức phương trình mặt cầu.

Lời giải chi tiết :

Bán kính của mặt cầu \(\left( S \right)\) là \(\sqrt {{2^2} + {1^2} - 3}  = \sqrt 2 \).

Câu 13 :

Cho \(P\left( A \right) = \frac{2}{7};P\left( {B|A} \right) = \frac{1}{4};P\left( {B|\overline A } \right) = \frac{1}{5}\). Giá trị của \(P\left( B \right)\) là

  • A

    \(\frac{1}{7}\).

  • B

    \(\frac{3}{{14}}\).

  • C

    \(\frac{1}{{14}}\).

  • D

    \(\frac{2}{7}\).

Đáp án : B

Phương pháp giải :

Áp dụng công thức xác suất toàn phần.

Lời giải chi tiết :

Ta có \(P\left( A \right) = \frac{2}{7} \Rightarrow P\left( {\overline A } \right) = \frac{5}{7}\).

Áp dụng công thức xác suất toàn phần

\(P\left( B \right) = P\left( A \right) \cdot P\left( {B|A} \right) + P\left( {\overline A } \right) \cdot P\left( {B|\overline A } \right) = \frac{2}{7} \cdot \frac{1}{4} + \frac{3}{7} \cdot \frac{1}{5} = \frac{3}{{14}}\).

Câu 14 :

Cho hai biến cố A, B sao cho \(P\left( A \right) = 0,4;P\left( {A|B} \right) = 0,7;P\left( {B|A} \right) = 0,3\). Tính \(P\left( {\overline B } \right)\)

  • A

    0,21.

  • B

    0,28.

  • C

    \(\frac{6}{{35}}\).

  • D

    \(\frac{{29}}{{35}}\).

Đáp án : D

Phương pháp giải :

Áp dụng công thức \(P\left( B \right) \cdot P\left( {A|B} \right) = P\left( A \right) \cdot P\left( {B|A} \right)\).

Lời giải chi tiết :

Ta có \(P\left( B \right) \cdot P\left( {A|B} \right) = P\left( A \right) \cdot P\left( {B|A} \right) \Rightarrow P\left( B \right) = 0,4 \cdot 0,3:0,7 = \frac{6}{{35}}\).

Câu 15 :

Họ nguyên hàm của hàm số \(f\left( x \right) = 3{x^2} + \sin x\) là

  • A

    \({x^3} + \cos x + C\).

  • B

    \(6x + \cos x + C\).

  • C

    \({x^3} - \cos x + C\).

  • D

    \(6x - \cos x + C\).

Đáp án : C

Phương pháp giải :

Áp dụng công thức tìm nguyên hàm cơ bản của hàm lũy thừa và hàm số lượng giác.

Lời giải chi tiết :

Ta có \(\int {f\left( x \right)dx}  = \int {\left( {3{x^2} + \sin x} \right)dx}  = \frac{{{x^3}}}{3} - \cos x + C\).

Câu 16 :

Cho \(\int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx}  = 5\). Tính \(I = \int\limits_0^{\frac{\pi }{2}} {\left[ {f\left( x \right) + 2\sin x} \right]dx} \).

  • A

    7.

  • B

    \(5 + \frac{\pi }{2}\).

  • C

    \(5 + \pi \).

  • D

    3.

Đáp án : A

Phương pháp giải :

Áp dụng tính chất phép cộng tích phân và các công thức nguyên hàm cơ bản.

Lời giải chi tiết :

Ta có \(I = \int\limits_0^{\frac{\pi }{2}} {\left[ {f\left( x \right) + 2\sin x} \right]dx}  = \int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx}  + 2\int\limits_0^{\frac{\pi }{2}} {\sin xdx}  = 5 - 2\left. {\cos x} \right|_0^{\frac{\pi }{2}} = 5 + 2 = 7\).

Câu 17 :

Biết \(\int\limits_1^3 {\frac{{x + 2}}{x}dx}  = a + b\ln c\), với \(a,b,c \in \mathbb{R},c > 0\). Tính tổng \(S = a + b + c\).

  • A

    5.

  • B

    6.

  • C

    7.

  • D

    8.

Đáp án : C

Phương pháp giải :

Tính tích phân \(\int\limits_1^3 {\frac{{x + 2}}{x}dx} \) từ đó suy ra \(a,b,c\).

Lời giải chi tiết :

Ta có \(\int\limits_1^3 {\frac{{x + 2}}{x}dx}  = \int\limits_1^3 {\left( {1 + \frac{2}{x}} \right)dx}  = \int\limits_1^3 {dx}  + 2\int\limits_1^3 {\frac{1}{x}dx}  = \left. x \right|_1^3 + 2\left. {\ln x} \right|_1^3 = 2 + 2\ln 3\) suy ra \(a = 2,b = 2,c = 3\).

Do đó \(S = a + b + c = 2 + 2 + 3 = 7\).

Câu 18 :

Cho hình phẳng D giới hạn bởi đồ thị hàm số  \(y = \sqrt {{x^2} + 1} \), trục hoành và hai đường thẳng \(x = 0,x = 1\). Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích là

  • A

    \(\frac{4}{3}\).

  • B

    \(\frac{{4\pi }}{3}\).

  • C

    \(2\pi \).

  • D

    2.

Đáp án : B

Phương pháp giải :

Áp dụng công thức tính thể tích khối tròn xoay ứng dụng tích phân.

Lời giải chi tiết :

Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích là

\(V = \pi \int\limits_0^1 {{{\left( {\sqrt {{x^2} + 1} } \right)}^2}dx}  = \pi \int\limits_0^1 {\left( {{x^2} + 1} \right)dx}  = \pi \left. {\left( {\frac{{{x^3}}}{3} + x} \right)} \right|_0^1 = \pi \left( {\frac{1}{3} + 1} \right) = \frac{{4\pi }}{3}\).

Câu 19 :

Cho hai mặt phẳng \(\left( \alpha  \right):3x - 2y + 2z + 7 = 0\), \(\left( \beta  \right):5x - 4y + 3z + 1 = 0\). Phương trình mặt phẳng đi qua gốc tọa độ O đồng thời vuông góc với cả hai mặt phẳng \(\left( \alpha  \right)\) và \(\left( \beta  \right)\) là

  • A

    \(2x - y - 2z = 0\).

  • B

    \(2x - y + 2z = 0\).

  • C

    \(2x + y - 2z = 0\).

  • D

    \(2x + y - 2z + 1 = 0\).

Đáp án : C

Phương pháp giải :

Xét 4 đáp án để kiểm tra mặt phẳng có đi qua O không. Tìm vectơ pháp tuyến của mặt

phẳng cần tìm bằng tích có hướng.

Lời giải chi tiết :

Đầu tiên ta loại đáp án D vì mặt phẳng \(2x + y - 2z + 1 = 0\) không đi qua O.

Hai mặt phẳng \(\left( \alpha  \right)\) và \(\left( \beta  \right)\) có các vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}}  = \left( {3; - 2;2} \right),\overrightarrow {{n_2}}  = \left( {5; - 4;3} \right)\).

Câu 20 :

Trong không gian Oxyz cho 3 điểm \(A\left( {1; - 2;3} \right),B\left( {2;0;1} \right),C\left( {3; - 2;0} \right)\). Phương trình mặt phẳng đi qua 3 điểm \(A,{\rm{ }}B,{\rm{ }}C\) là

  • A

    \(6x + y - 4z = 16\).

  • B

    \(6x - y - 4z = 16\).

  • C

    \(6x + y + 4z = 16\).

  • D

    \(6x - y + 4z = 16\).

Đáp án : C

Phương pháp giải :

Tìm vectơ pháp tuyến của mặt phẳng cần tìm bằng tích có hướng.

Lời giải chi tiết :

Ta có  \(\overrightarrow {AB}  = \left( {1;2; - 2} \right),\overrightarrow {AC}  = \left( {2;0; - 3} \right)\).

Suy ra vectơ pháp tuyến của mặt phẳng đi qua 3 điểm \(A,{\rm{ }}B,{\rm{ }}C\) là

\(\overrightarrow n  = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 6; - 1; - 4} \right) =  - \left( {6;1;4} \right)\). Do đó ta chọn C.

Câu 21 :

Trong không gian Oxyz cho điểm \(A\left( {1;2; - 1} \right)\) và mặt phẳng \(\left( P \right):x + 3y - 2z - 1 = 0\). Phương trình đường thẳng đi qua điểm \(A\) và vuông góc với mặt phẳng \(\left( P \right)\) là

  • A

    \(\frac{{x + 1}}{1} = \frac{{y + 2}}{3} = \frac{{z - 1}}{{ - 2}}\).

  • B

    \(\frac{{x - 1}}{1} = \frac{{y - 2}}{3} = \frac{{z + 1}}{{ - 2}}\).

  • C

    \(\frac{{x + 1}}{{ - 1}} = \frac{{y + 2}}{{ - 3}} = \frac{{z - 1}}{{ - 2}}\).

  • D

    \(\frac{{x - 1}}{1} = \frac{{y - 2}}{3} = \frac{{z + 1}}{2}\).

Đáp án : B

Phương pháp giải :

Loại các đáp án có đường thẳng không đi qua A. Đường thẳng cần tìm có một vectơ chỉ

phương là vectơ pháp tuyến của mặt phẳng (P).

Lời giải chi tiết :

Ta loại đáp án A và C do hai đường thẳng này đều không đi qua A.

Mặt phẳng \(\left( P \right)\) có một vectơ pháp tuyến là \(\overrightarrow n  = \left( {1;3; - 2} \right)\), vectơ này cũng là một vectơ chỉ phương của đường thẳng đi qua điểm \(A\) và vuông góc với mặt phẳng \(\left( P \right)\).

Câu 22 :

Trong không gian Oxyz cho hai điểm \(M\left( {1;0;1} \right)\) và \(N\left( {3;2; - 1} \right)\). Đường thẳng \(MN\) có phương trình tham số là

  • A

    \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2t\\z = 1 + t.\end{array} \right.\)

  • B

    \(\left\{ \begin{array}{l}x = 1 + t\\y = t\\z = 1 + t.\end{array} \right.\)

  • C

    \(\left\{ \begin{array}{l}x = 1 + t\\y = t\\z = 1 - t.\end{array} \right.\)

  • D

    \(\left\{ \begin{array}{l}x = 1 - t\\y = t\\z = 1 + t.\end{array} \right.\)

Đáp án : C

Phương pháp giải :

Vì 4 đáp án đều có các vectơ chỉ phương không cùng phương nên ta chỉ cần xác định vectơ

chỉ phương của \(MN\) và đối chiếu với các đáp án.

Lời giải chi tiết :

Ta có \(\overrightarrow {MN}  = \left( {2;2; - 2} \right)\) là một vectơ chỉ phương của đường thẳng \(MN\).

Câu 23 :

Trong không gian Oxyz cho hai điểm \(A\left( {2;4;1} \right)\) và \(B\left( { - 2;2; - 3} \right)\). Phương trình mặt cầu đường kính \(AB\) là

  • A

    \({x^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 9\).

  • B

    \({x^2} + {\left( {y - 3} \right)^2} + {\left( {z - 1} \right)^2} = 36\).

  • C

    \({x^2} + {\left( {y + 3} \right)^2} + {\left( {z - 1} \right)^2} = 9\).

  • D

    \({x^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 36\).

Đáp án : A

Phương pháp giải :

Xác định tâm và bán kính mặt cầu.

Lời giải chi tiết :

Mặt cầu cần tìm có tâm là trung điểm \(I\left( {0;3; - 1} \right)\) của đoạn \(AB\).

Bán kính mặt cầu là \(IA = \sqrt {4 + 1 + 4}  = 3\).

Suy ra phương trình mặt cầu là \({x^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 9\).

Câu 24 :

Sử dụng dữ kiện sau để trả lời:

Bạn An có một túi gồm 8 viên bi đen và 6 viên bi trắng. An lấy ngẫu nhiên một viên bi trong túi để cho Việt, rồi lại lấy ngẫu nhiên tiếp một viên bi nữa trong túi và cũng đưa cho Việt.

Xác suất để Việt nhận được 2 viên bi trắng là

  • A

    \(\frac{3}{7}\).

  • B

    \(\frac{{15}}{{91}}\).                   

  • C

    \(\frac{{30}}{{91}}\).

  • D

    \(\frac{{15}}{{182}}\).

Đáp án : B

Phương pháp giải :

Đặt tên các biến cố và áp dụng công thức xác suất có điều kiện.

Lời giải chi tiết :

Gọi C là biến cố: “Hai viên bi Việt nhận được đều là trắng”.

       A là biến cố: “Viên bi đầu tiên An lấy được là trắng”.

       B là biến cố: “Viên bi thứ hai An lấy được là trắng”. 

Khi đó \(C = AB\). Ta có \(P\left( A \right) = \frac{6}{{14}}\), \(P\left( {B|A} \right) = \frac{5}{{13}}\).

Suy ra \(P\left( C \right) = P\left( {AB} \right) = P\left( A \right) \cdot P\left( {B|A} \right) = \frac{6}{{14}} \cdot \frac{5}{{13}} = \frac{{15}}{{91}}\).

Câu 25 :

Sử dụng dữ kiện sau để trả lời:

Bạn An có một túi gồm 8 viên bi đen và 6 viên bi trắng. An lấy ngẫu nhiên một viên bi trong túi để cho Việt, rồi lại lấy ngẫu nhiên tiếp một viên bi nữa trong túi và cũng đưa cho Việt.

Xác suất để Việt nhận được viên bi đen ở lần thứ nhất và viên bi trắng ở lần thứ hai là

  • A

    \(\frac{3}{7}\).

  • B

    \(\frac{{15}}{{91}}\).

  • C

    \(\frac{{30}}{{91}}\).

  • D

    \(\frac{{15}}{{182}}\).

Đáp án : A

Phương pháp giải :

Đặt tên các biến cố và xác định biến cố cần tính xác suất. Áp dụng công thức xác suất có

điều kiện.

Lời giải chi tiết :

Gọi A là biến cố: “Viên bi đầu tiên An lấy được là đen”.

       B là biến cố: “Viên bi thứ hai An lấy được là trắng”. 

Khi đó \(P\left( A \right) = \frac{8}{{14}},P\left( {B|A} \right) = \frac{6}{{13}}\).

Ta cần tính \(P\left( {AB} \right)\). Ta có \(P\left( {AB} \right) = P\left( A \right)P\left( {B|A} \right) = \frac{8}{{14}} \cdot \frac{6}{{13}} = \frac{{24}}{{91}}\).

Câu 26 :

Một xạ thủ bắn vào bia số 1 và bia số 2. Xác suất để xạ thủ đó bắn trúng bia số 1 là 0,8 và bắn trúng bia số 2 là 0,9. Xác suất để xạ thủ đó bắn trúng cả hai bia là 0,75. Biết xạ thủ đó bắn không trúng bia số 1, xác suất để xạ thủ đó bắn trúng bia số 2 là

  • A

    \(\frac{{41}}{{50}}\).

  • B

    \(\frac{9}{{50}}\).

  • C

    \(\frac{1}{4}\).

  • D

    \(\frac{3}{4}\).

Đáp án : D

Phương pháp giải :

Đặt tên các biến cố và xác định biến cố cần tính xác suất. Áp dụng công thức xác suất có

điều kiện.

Lời giải chi tiết :

Gọi A là biến cố: “Xạ thủ đó bắn trúng bia số 1”.

       B là biến cố: “Xạ thủ đó bắn trúng bia số 2”. 

Biết xạ thủ đó bắn không trúng bia số 1, xác suất để xạ thủ đó bắn trúng bia số 2 là

\(P\left( {B|\overline A } \right) = \frac{{P\left( {B\overline A } \right)}}{{P\left( {\overline A } \right)}} = \frac{{P\left( B \right) - P\left( {BA} \right)}}{{1 - P\left( A \right)}} = \frac{{0,9 - 075}}{{1 - 0,8}} = \frac{3}{4}\).

Câu 27 :

Họ nguyên hàm của hàm số \(y = {e^x}\left( {2 + \frac{{{e^{ - x}}}}{{{{\cos }^2}x}}} \right)\) là

  • A

    \(2{e^x} - \frac{1}{{\cos x}} + C\).

  • B

    \(2{e^x} - \tan x + C\).

  • C

    \(2{e^x} + \tan x + C\).

  • D

    \(2{e^x} + \frac{1}{{\cos x}} + C\).

Đáp án : C

Phương pháp giải :

Áp dụng các công thức tìm nguyên hàm cơ bản.

Lời giải chi tiết :

Ta có \(\int {{e^x}\left( {2 + \frac{{{e^{ - x}}}}{{{{\cos }^2}x}}} \right)dx}  = 2\int {{e^x}dx}  + \int {\frac{{dx}}{{{{\cos }^2}x}}}  = 2{e^x} + \tan x + C\).

Câu 28 :

Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau \(\left( {{x_0};{p_0}} \right)\) của đồ thị hàm cầu \(y = D\left( x \right)\) và đồ thị hàm cung \(p = S\left( x \right)\) được gọi là điểm cân bằng. Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang \(p = {p_0}\) và đường thẳng đứng \(x = 0\) là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị hàm cung, đường nằm ngang \(p = {p_0}\) và đường thẳng đứng \(x = 0\) được gọi là thặng dư sản xuất, như hình vẽ sau:

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: \(y =  - 0,01{e^x} + 19\) và hàm cung \(p = 0,09{e^x} + 1\) trong đó \(x\) là số đơn vị sản phẩm. Thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này lần lượt là (làm tròn kết quả đến chữ số thập phân thứ hai)?

  • A

    68,01 và 7,57.

  • B

    68,02 và 7,56.

  • C

    69,02 và 7,56.

  • D

    70,02 và 7,66.

Đáp án : B

Phương pháp giải :

Tìm tọa độ điểm cân bằng. Áp dụng công thức tìm thặng dư tiêu dùng và thặng dư sản

xuất theo tích phân.

Lời giải chi tiết :

Hoành độ điểm cân bằng là nghiệm của phương trình

\( - 0,01{e^x} + 19 = 0,09{e^x} + 1 \Rightarrow 0,1{e^x} = 18 \Rightarrow x = \ln 180\).

Suy ra tung độ điểm cân bằng là \(y = 0,09{e^{\ln 180}} + 1 = 17,2\).

Thặng dư sản xuất cho sản phẩm đã cho là \(\int\limits_0^{\ln 180} {\left| {17,2 - 0,09{e^x} - 1} \right|dx}  \approx 68,02\).

Thặng dư tiêu dùng cho sản phẩm đã cho là \(\int\limits_0^{\ln 180} {\left| { - 0,01{e^x} + 19 - 17,2} \right|dx}  \approx 7,56\).

Câu 29 :

Một ô tô đang chạy với vận tốc 10 m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) =  - 5t + 10\) (m/s), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

  • A

    0,2 m.

  • B

    2 m.  

  • C

    10 m.

  • D

    20 m.

Đáp án : C

Phương pháp giải :

Quãng đường cần tìm là tích phân của vận tốc từ 0 đến 2.

Lời giải chi tiết :

Xét phương trình \( - 5t + 10 = 0 \Leftrightarrow t = 2\).

Do vậy, kể từ lúc người lái đạp phanh thì sau 2 giây ô tô dừng hẳn.

Quãng đường ô tô đi được kể từ lúc người lái đạp phanh đến khi ô tô dừng hẳn là

\(s = \int\limits_0^2 {\left( { - 5t + 10} \right)dt}  = \left. {\left( { - \frac{5}{2}{t^2} + 10t} \right)} \right|_0^2 = 10\) (m).

Câu 30 :

Góc quan sát ngang của một camera là \({130^ \circ }\). Trong không gian \(Oxyz\), camera được đặt tại điểm \(C\left( {1;2;2} \right)\) và chiếu thẳng về phía mặt phẳng \(\left( P \right):x + 2y - 2z + 5 = 0\). Hỏi vùng quan sát được trên mặt phẳng \(\left( P \right)\) của camera là hình tròn có diện tích bằng bao nhiêu? (làm tròn kết quả đến chữ số thập phân thứ nhất).

  • A

    57,7.

  • B

    57,8.

  • C

    56,7. 

  • D

    56,8.

Đáp án : B

Phương pháp giải :

Tìm bán kính vùng quan sát thông qua khoảng cách từ điểm \(C\) tới mặt phẳng \(\left( P \right)\).

Lời giải chi tiết :

Gọi \(H\) là hình chiếu của \(C\) trên mặt phẳng \(\left( P \right)\). Khoảng cách từ điểm \(C\) tới mặt phẳng \(\left( P \right)\) là \(d\left( {C,\left( P \right)} \right) = CH = \frac{{\left| {1 + 4 - 4 + 5} \right|}}{{\sqrt {1 + {2^2} + {2^2}} }} = 2\).

Vùng quan sát là hình tròn tâm \(H\) bán kính \(HA\) và có diện tích là \(\pi  \cdot {\left( {CH \cdot \tan {{65}^ \circ }} \right)^2} \approx 57,8\).

Câu 31 :

Trong không gian \(Oxyz\), cho các đường thẳng:

\(\left( {{d_1}} \right):\frac{{x - 3}}{1} = \frac{{y + 1}}{{ - 2}} = \frac{{z + 1}}{1}\),                               \(\left( {{d_2}} \right):\frac{x}{1} = \frac{y}{{ - 2}} = \frac{{z - 1}}{1}\),

\(\left( {{d_3}} \right):\frac{{x - 1}}{1} = \frac{{y + 1}}{1} = \frac{{z - 1}}{1}\),                                \(\left( {{d_4}} \right):\frac{x}{1} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 1}}{1}\).

Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là

  • A

    1.

  • B

    2.

  • C

    0.

  • D

    Vô số.

Đáp án : A

Phương pháp giải :

Xét vị trí tương đối của 4 đường thẳng với nhau để đưa ra nhận xét.

Lời giải chi tiết :

Ta có \({d_1}\parallel {d_2}\) nên chúng xác định duy nhất một mặt phẳng \(\left( P \right)\). Giả sử có đường thẳng cắt cả 4 đường thẳng đề bài cho thì nó phải thuộc \(\left( P \right)\). Kiểm tra được các đường thẳng \({d_3},{d_4}\) cắt \(\left( P \right)\) lần lượt tại A, B.

Vậy có duy nhất đường thẳng AB cắt cả 4 đường thẳng đã cho.

Câu 32 :

Biết rằng nếu vị trí \(M\) có vĩ độ và kinh độ tương ứng là \({\alpha ^ \circ }N,{\beta ^ \circ }E\left( {0 < \alpha ,\beta  < 90} \right)\) thì có tọa độ \(M\left( {\cos {\alpha ^ \circ }\cos {\beta ^ \circ };\cos {\alpha ^ \circ }\sin {\beta ^ \circ };\sin {\alpha ^ \circ }} \right)\). Biết một đơn vị dài trong không gian \(Oxyz\) tương ứng với 6371 km trong thực tế. Khoảng cách trên mặt đất từ vị trí \(P:{30^ \circ }N{45^ \circ }E\) đến vị trí \(Q:{60^ \circ }N{45^ \circ }E\) là (tính chính xác tới chữ số thập phân thứ 4 sau dấu phẩy theo đơn vị kilômét)?

  • A

    3335,8475 km.

  • B

    3335,8478 km.

  • C

    3355,8478 km.

  • D

    3355,8475 km.

Đáp án : B

Phương pháp giải :

Xác định tọa độ \(P,{\rm{ }}Q\). Từ đó xác định \(\widehat {POQ}\).

Lời giải chi tiết :

Ta có \(P\left( {\frac{{\sqrt 6 }}{4};\frac{{\sqrt 6 }}{4};\frac{1}{2}} \right),{\rm{ }}Q\left( {\frac{{\sqrt 2 }}{4};\frac{{\sqrt 2 }}{4};\frac{{\sqrt 3 }}{2}} \right)\).

Từ đó \(\cos \widehat {POQ} = \frac{{\overrightarrow {OP}  \cdot \overrightarrow {OQ} }}{{\left| {\overrightarrow {OP} } \right| \cdot \left| {\overrightarrow {OQ} } \right|}} = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat {POQ} = {30^ \circ }\).

Khoảng cách trên mặt đất từ \(P\) đến \(Q\) là \(\frac{{30 \cdot 2\pi }}{{360}} \cdot 6371 \approx 3335,8478\).

Câu 33 :

Có hai chuồng thỏ. Chuồng I có 6 con thỏ đen và 10 con thỏ trắng. Chuồng II có 8 con thỏ đen và 4 con thỏ trắng. Trước tiên, từ chuồng I lấy ra ngẫu nhiên một con thỏ rồi cho vào chuồng II. Sau đó, từ chuồng II lấy ra ngẫu nhiên một con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng.

  • A

    \(\frac{5}{{13}}\).

  • B

    \(\frac{{37}}{{104}}\).

  • C

    \(\frac{4}{{13}}\).

  • D

    \(\frac{{35}}{{104}}\).

Đáp án : B

Phương pháp giải :

Gọi tên các biến cố, áp dụng công thức xác suất toàn phần.

Lời giải chi tiết :

Gọi biến cố A: “Lấy từ chuồng I ra được thỏ trắng”;

                    B: “Lấy từ chuồng II ra được thỏ trắng”.

Ta có \(P\left( A \right) = \frac{{10}}{{16}};P\left( {\overline A } \right) = \frac{6}{{16}};P\left( {B|A} \right) = \frac{5}{{13}};P\left( {B|\overline A } \right) = \frac{4}{{13}}\).

Vậy \(P\left( B \right) = P\left( A \right) \cdot P\left( {B|A} \right) + P\left( {\overline A } \right) \cdot P\left( {B|\overline A } \right) = \frac{{10}}{{16}} \cdot \frac{5}{{13}} + \frac{6}{{16}} \cdot \frac{4}{{13}} = \frac{{37}}{{104}}\).

Câu 34 :

Giả sử có một loại bệnh mà tỉ lệ người mắc bệnh là 0,01%. Nếu một người mắc bệnh thì xác suất xét nghiệm cho kết quả dương tính là 90%, nếu một người không mắc bệnh thì xác suất cho kết quả dương tính là 5%. Khi một người xét nghiệm có kết quả dương tính thì khả năng mắc bệnh của người đó là bao nhiêu phần trăm?

  • A

    0,01%.  

  • B

    4,9995%.

  • C

    0,1797%.

  • D

    0,001%.

Đáp án : C

Phương pháp giải :

Gọi tên các biến cố, áp dụng công thức Bayes.

Lời giải chi tiết :

Gọi biến cố M: “Người đó mắc bệnh”;

                    D: “Người đó xét nghiệm dương tính”.

Ta có \(P\left( M \right) = 0,01\%  = 0,0001 \Rightarrow P\left( {\overline M } \right) = 1 - 0,0001 = 0,9999\).

Trong số những người không mắc bệnh nhưng có 5% số người có xét nghiệm dương tính

nên \(P\left( {D|\overline M } \right) = 5\%  = 0,05\).

Nếu một người mắc bệnh thì xác suất xét nghiệm cao cho kết quả dương tính là 90% nên

\(P\left( {D|M} \right) = 90\%  = 0,9\).

Khi một người xét nghiệm có kết quả dương tính thì khả năng mắc bệnh của người đó là

\(P\left( {M|D} \right)\). Áp dụng công thức Bayes ta có

\(P\left( {M|D} \right) = \frac{{P\left( M \right) \cdot P\left( {D|M} \right)}}{{P\left( M \right) \cdot P\left( {D|M} \right) + P\left( {\overline M } \right) \cdot P\left( {D|\overline M } \right)}} = \frac{{0,0001 \cdot 0,9}}{{0,0001 \cdot 0,9 + 0,9999 \cdot 0,05}} = 0,1797\% \).

Câu 35 :

Có hai đội thi đấu môn bắn súng. Đội I có 6 vận động viên, đội II có 8 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên trong hai đội. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I.

  • A

    \(\frac{{39}}{{140}}\).  

  • B

    \(\frac{{39}}{{83}}\).

  • C

    \(\frac{{43}}{{83}}\).

  • D

    \(\frac{{37}}{{140}}\).

Đáp án : B

Phương pháp giải :

Gọi tên các biến cố, áp dụng công thức Bayes.

Lời giải chi tiết :

Gọi biến cố A: “Vận động viên được chọn thuộc đội I”;

                    V: “Vận động viên đạt huy chương vàng”.

Ta có \(P\left( A \right) = \frac{6}{{14}} = \frac{3}{7} \Rightarrow P\left( {\overline A } \right) = 1 - P\left( A \right) = \frac{4}{7}\);\(P\left( {V|A} \right) = 0,65;P\left( {V|\overline A } \right) = 0,55\).

Xác suất để vận động viên thuộc đội I khi đạt huy chương vàng là

\(P\left( {A|V} \right) = \frac{{P\left( A \right) \cdot P\left( {V|A} \right)}}{{P\left( A \right) \cdot P\left( {V|A} \right) + P\left( {\overline A } \right) \cdot P\left( {V|\overline A } \right)}} = \frac{{\frac{3}{7} \cdot 0,65}}{{\frac{3}{7} \cdot 0,65 + \frac{4}{7} \cdot 0,55}} = \frac{{39}}{{83}}\).

Phần II: Tự luận.
Thí sinh trả lời từ câu 36 đến câu 38.
Câu 1 :

Hình bên dưới là một cánh cửa gỗ, phần dưới có dạng hình chữ nhật \(ABCD\) và mép trên là một phần của đường parabol với kích thước như sau: \(AB = 2,2m,{\rm{ }}AD = 4m,{\rm{ }}EO = 5,5m\). Biết giá thành sản xuất cửa là \(30\) triệu đồng\(/{m^2}\). Tính tổng chi phí để sản xuất cửa gỗ đã cho (làm tròn tới chữ số hàng phần trăm của triệu đồng).
Phương pháp giải :

Chọn hệ trục tọa độ phù hợp và gắn tọa độ cho các điểm. Tính diện tích hình phẳng bằng

ứng dụng tích phân.

Lời giải chi tiết :

Chọn hệ trục Oxyz sao cho \(A\left( { - 1;1;0} \right),{\rm{ }}B\left( {1;1;0} \right)\), khi đó ta có

\(C\left( {1;1;4} \right),{\rm{ }}D\left( { - 1;1;4} \right),{\rm{ }}E\left( {0;5;5} \right)\).

Phương trình của parabol có dạng \(\left( P \right):y = a{x^2} + bx + c\). Do \(\left( P \right)\) đi qua \(C,D,E\) nên có

phương trình \(y =  - \frac{{150}}{{121}}{x^2} + 1,5\).

Vậy diện tích cánh cửa gỗ là \(2,2 \cdot 4 + \int\limits_{ - 1,1}^{1,1} {\left| { - \frac{{150}}{{121}}{x^2} + 1,5} \right|dx = 11\left( {{m^2}} \right)} \).

Câu 2 :

Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x + 2y - 2z + 3 = 0\) và đường thẳng

\(d:\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{z}{1}\). Tính góc tạo bởi đường thẳng \(d\) và mặt phẳng \(\left( P \right)\).
Phương pháp giải :

Áp dụng công thức liên hệ tích vô hướng của hai vectơ để tính sin.

Lời giải chi tiết :

Ta có một vectơ pháp tuyến của \(\left( P \right)\) là \(\overrightarrow n  = \left( {1;2; - 2} \right)\); một vectơ chỉ phương của \(d\) là \(\overrightarrow u  = \left( {2; - 1;1} \right)\). Suy ra \(\sin \left( {d,\left( P \right)} \right) = \frac{{\left| {\overrightarrow n  \cdot \overrightarrow u } \right|}}{{\left| {\overrightarrow n } \right| \cdot \left| {\overrightarrow u } \right|}} = \frac{{\left| {2 - 2 - 2} \right|}}{{3\sqrt 6 }} = \frac{2}{{3\sqrt 6 }} \Rightarrow \left( {d,\left( P \right)} \right) \approx 15,{79^ \circ }\).

Câu 3 :

Trong một hộp kín có 10 chiếc bút bi xanh và 6 chiếc bút bi đỏ đều có kích thước và khối lượng như nhau. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi từ trong hộp, không trả lại. Sau đó bạn Tùng lấy ngẫu nhiên một trong 15 chiếc bút còn lại. Tính xác suất bạn Sơn lấy được chiếc bút bi xanh và Tùng lấy được chiếc bút bi đỏ.
Phương pháp giải :

Áp dụng công thức nhân xác suất.

Lời giải chi tiết :

Gọi A là biến cố: “Bạn Sơn lấy được chiếc bút bi xanh”;

       B là biến cố: “Bạn Tùng lấy được chiếc bút bi đỏ”;

Vì \(n\left( A \right) = 10\) nên \(P\left( A \right) = \frac{{10}}{{16}} = \frac{5}{8}\).

Nếu A xảy ra tức là Sơn lấy được chiếc bút bi xanh thì trong hộp còn lại 9 chiếc bút bi

xanh và 6 chiếc bút bi đỏ. Suy ra \(P\left( {B|A} \right) = \frac{6}{{15}}\).

Theo công thức nhân xác suất \(P\left( {AB} \right) = P\left( A \right) \cdot P\left( {B|A} \right) = \frac{5}{8} \cdot \frac{6}{{15}} = \frac{1}{4}\).

Vậy xác suất cần tìm là \(\frac{1}{4}\).

Bài liên quan
close